Proof: Coordinate Rotation Around (0,0)

[Maybe_Memorie]

Homework Statement

Prove that the coordinates of the point (x',y') where the counter-clockwise rotation through the angle @ around (0,0) brings the given point (x,y) are

x' = xcos@ - ysin@
y' = xsin@ + ycos@

Hint: show that for the points (x,y) = (1,0) and (x,y) = (0,1) directly,
and use the fact that the vector (x,y) is equal to the combination
x.(1,0) + y.(0,1)

Homework Equations

For vectors u and v, angle @ between them
u.v = |u||v|Cos@

The Attempt at a Solution

I don't want to be told how to do it, I would prefer if someone would kind of tease the solution out of me, if you know what i mean..

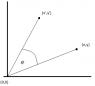
I've included a diagram, showing my interpretation of the question.

I've tried a few different approaches for the question.
I used the fact that tan@ = (m1 - m2)/(1 +m1m2).
I got the slopes of the lines being y/x and y'/x'. When I plugged everything in and rewrote tan as sin/cos, I got the required formulae, but they were both being divided by each other.

I also used the dot product, put this just resulted with a lot of squares which doesn't help.

I don't entirely understand the hint also.

 

[gerben]

Use the hint that was given.

First draw a rectangle with corners (0,0) and (x,y) (with sides parallel to x- and y-axis) and then draw the rectangle that you get when the whole plane is rotated by an angle @.

Then you can see in your drawing that the new x' and y' are just sums of the height and width of the rectangle multiplied by sines and/or cosines of @

 

[Maybe_Memorie]

I don't really understand what the hint means.

Okay, I'll try that.

 

[JThompson]

The hint is basically saying that if your starting vectors are either

$$\left(\begin{array}{c}1\\0\end{array}\right)\mbox{ or }\left(\begin{array}{c}0\\1\end{array}\right)$$

then it's pretty easy to figure out what the new coordinates will be if you rotate it through an angle $$\theta$$.

You'll need the sum of angles formulas for cos and sin, $$\cos(\theta_{0}+\theta)$$ and $$\sin(\theta_{0}+\theta)$$.
($$\theta_{0}$$ is the initial trig angle for the vector).

Does this make sense?

 

[Maybe_Memorie]

It makes sense, but I have no idea where to start.

 

[gerben]

You original vector is:

$$v = a\cdot \left(\begin{array}{c}1\\0\end{array}\right) + b\cdot \left(\begin{array}{c}0\\1\end{array}\right)$$

so the rotated vector will be:

$$rot_\theta(v) = a \cdot rot_\theta (\left(\begin{array}{c}1\\0\end{array}\right) ) + b\cdot rot_\theta ( \left(\begin{array}{c}0\\1\end{array}\right) )$$

You can first determine c and d in:

$$rot_\theta (\left(\begin{array}{c}1\\0\end{array}\right) ) = c\cdot \left(\begin{array}{c}1\\0\end{array}\right) + d\cdot \left(\begin{array}{c}0\\1\end{array}\right)$$

and e and f in:

$$rot_\theta (\left(\begin{array}{c}0\\1\end{array}\right) ) = e\cdot \left(\begin{array}{c}1\\0\end{array}\right) + f\cdot \left(\begin{array}{c}0\\1\end{array}\right)$$

and then substitute those in your expression for $$rot_\theta(v)$$.