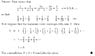vg19
- 67
- 0
Homework Statement
Prove the divergence of the harmonic series by contridiction
Homework Equations
Attached file
The Attempt at a Solution
I understand what they are doing in the first two lines, however, the lines after assuming the series converges with sum S, confuses me. They list the harmonic series and are adding terms in sets of three. I can't see where the next line comes from ( > 1 + 3/3 + 3/6 + 3/9).
Would somebody please be able to help me understand this proof?
Thanks