The_Logos
- 8
- 0
Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalence
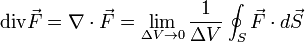 true?
true?
The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.The_Logos said:Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalencetrue?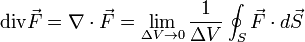
mathman said:
zoki85 said:The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.
Suppose p is a point in 3D Euclidean space. Let Er be a solid ball centered at p with radius r , and let Sr be the boundary surface of Er with outward pointing normal (and F is the vector field). Using Gauss' theorem we have:
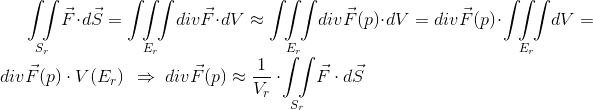
This aproximation improves as radius gets smaller, and in the limit (for r → 0 ⇒ Vr → 0) the equality holds.
Hope this helps.
Meh, my "logos" is quite irrational in everyday life, so I don't think that user name would suit me fine. And, althought short, this is kind of a sloppy proof. It's more a demonstration by Gauss' D.T. why it holds true. I guess a pro-mathematcian should feel a need to "polish" it, to write more rigouros proof. I agree there must be other ways to prove the formula (without G.D.T.) but I didn't try it.The_Logos said:That is just beautiful! you should just go ahead and take my user name, you are definitely more the logos than me! I wasted all day trying to make linear transformations thinking that it was my only hope (And managed nothing).
I actually was seeking for the proof of the equivalence before giving deep thought to the divergence theorem, just to find out that ironically I needed it to prove what apparently came before!.