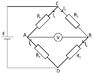
whatdoido
- 48
- 2
Homework Statement
Prove the following equation:
## \Delta U=\frac {R_1R_4}{(R_1+R_4)^2}(\frac {\Delta R_1}{R_1}-\frac {\Delta R_2}{R_2}+\frac{\Delta R_3}{R_3}-\frac{\Delta R_4}{R_4})E##
This is used in Wheatstone bridge
Homework Equations
[/B]
U=RI
The Attempt at a Solution
This has been a real head-scratcher
Two voltage dividers can be found for starters. Voltage's direction is assumed to be clockwise
##V_{in1}=I_2(R_2+R_3)##
##I_2=\frac{V_{in1}}{R_2+R_3}##
##V_{out1}=I_2R_3##
##V_{out1}=V_{in1}\frac{R_3}{R_2+R_3}##
Similarly:
##V_{out2}=V_{in1}\frac{R_4}{R_1+R_4}##
##V_G## is voltage between A and B
##V_{out1}-V_{out2}=V_G##
##V_{in1}\frac{R_3}{R_2+R_3}-V_{in1}\frac{R_4}{R_1+R_4}=V_G##
##V_{in1}(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=V_G##
##V_{in1}=E##
##V_G=\Delta U## so then
##E(\frac{R_3}{R_2+R_3}-\frac{R_4}{R_1+R_4})=\Delta U##
I have calculated voltages in different circuits and tried to think this problem in different ways, but the real problem is that how is ##\Delta R_i## inserted into equations. Assumption goes that it is added by ##R_i+\Delta R_i##. Maybe that is incorrect?
Help is very much appreciated!
edit: Misspelling corrected
Also particularizing that ##\Delta R_i## is a change in one resistance
Attachments
Last edited: