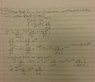Proofs with current density and wavefunctions

[Mary]

Homework Statement

So I was able to find a problem that was kind of similar to a homework problem that I am working on. Unfortunately, I'm not quite sure what is going on partially within the problem.

In the problem they state that $\phi$=$\phi$*, but it does not state why. I was wondering if someone could explain this to me?

Also, later on in the problem e$^{-i\phi}$e$^{i\phi}$+e$^{i\phi}$e$^{-i\phi}$ cancels out along with the 1/2i. I'm not quite sure how this happened either. I have tried to review the euler's equation to understand where this comes from because I'm supposing it is being canceled out based on its properties.

I have attached the proof to this forum.


I would greatly appreciate some help because the problem I am working on involves proving that the integral of the current density over a surface is equal to the momentum operator/m. I understand conceptually what this means but I need a push in the write direction with the math behind it.

 

[MisterX]

You seem to be missing a factor of $i$ when you plug back in. The $i$ factors come from the $\frac{\partial}{\partial x}$.

Also,

$e^{i\phi}e^{-i\phi} = e^{0} = 1$.

This comes from the properties of exponentials, but you can show this using Euler's formula as well. Note $\left(a + ib\right)\left(a-ib\right) = a^2 + b^2$, and $\sin\left(-\phi\right) = -\sin\phi$.