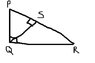
Prove triangle PQS is similar to triangle QRS

  • Thread starter Thread starter aricho
  • Start date Start date
  • Tags Tags
    Triangle
AI Thread Summary
Triangle PQS is similar to triangle QRS because they share angle Q and have two pairs of complementary angles: angles QPS and QRS, as well as angles QQS and PQS. The similarity of the triangles can be established by noting that they contain the same three angles. Consequently, the relationship QS^2 = PS * SR can be derived from the properties of similar triangles. This conclusion relies on the fundamental principle that similar triangles maintain proportional relationships between their corresponding sides. Understanding these angle relationships is crucial for proving the similarity and subsequent equations.
aricho
Messages
71
Reaction score
0
I'm having trouble doing this...

prove triangle PQS is similar to triangle QRS
Hence prove QS^2=PS.SR

the diagram is attached

cheers
 

Attachments

  • tri.JPG
    tri.JPG
    9.7 KB · Views: 468
Physics news on Phys.org
Look at the angles. angles QPS and QRS are complementary. So are QQS and PQS.
 
yer, but how can u prove that they triangles are similar?
 
If two triangles contain the same three angles, then they are similar.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

How do we represent a triangle wave for input voltage in this circuit?
Replies
3
Views
745
B More similar triangle problems
Replies
16
Views
573
Estimating the velocity of seismic waves through an idealized Earth
Replies
6
Views
2K
1st year high school geometry proof
Replies
14
Views
1K
Moment of inertia of an isosceles triangle
Replies
13
Views
4K
Help Me Solve My Diagram Problem: Calculating Center of Mass
Replies
8
Views
2K
To find the center of gravity of a particular quadrilateral
Replies
12
Views
3K
Solving a Vector Triangle Differential Equation
Replies
3
Views
1K
Two candles making shadows of one another on opposite walls
Replies
3
Views
1K
Electric Field of Equilateral Triangle
Replies
2
Views
4K

Hot Threads

Recent Insights

Back
Top