IlyaMath
- 3
- 0
I am having trouble proving that two multivariate formulas are equivalent. I implemented them in MATLAB and numerically they appear to be equivalent.
I would appreciate any help on this.
Prove A = B
A = (Σπ^-1 + Σy^-1)^-1 * (Σπ^-1*π + Σy^-1*y)
y = π+ X*β
Σπ =τ*Σ
Σy = X' * Σβ * X + ΣεB = (Σπ^-1 + P'*Σβ^-1*P)^-1 * (Σπ^-1*π + P'*Σβ^-1*q)
q = P*y
P = (X'*Σ^-1*X)^-1*X'*Σ^-1Assumptions
i) Σε is infinitesimally small. (If Σε is exactly zero, then Σy may not be invertible).
ii) N > F (If N = F, then the proof is trivial. If N < F then is probably not invertible and P is not defined.)Notation
A, B: Nx1
π: Nx1
y: Nx1
q: Fx1
β: Fx1
Σ: NxN
Σπ: NxN
Σy: NxN
Σβ: FxF
Σε: NxN
X: NxF
P: FxN
τ: 1x1
I would appreciate any help on this.
Prove A = B
A = (Σπ^-1 + Σy^-1)^-1 * (Σπ^-1*π + Σy^-1*y)
y = π+ X*β
Σπ =τ*Σ
Σy = X' * Σβ * X + ΣεB = (Σπ^-1 + P'*Σβ^-1*P)^-1 * (Σπ^-1*π + P'*Σβ^-1*q)
q = P*y
P = (X'*Σ^-1*X)^-1*X'*Σ^-1Assumptions
i) Σε is infinitesimally small. (If Σε is exactly zero, then Σy may not be invertible).
ii) N > F (If N = F, then the proof is trivial. If N < F then is probably not invertible and P is not defined.)Notation
A, B: Nx1
π: Nx1
y: Nx1
q: Fx1
β: Fx1
Σ: NxN
Σπ: NxN
Σy: NxN
Σβ: FxF
Σε: NxN
X: NxF
P: FxN
τ: 1x1
Attachments
-
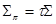 upload_2015-7-1_17-3-58.png314 bytes · Views: 551
upload_2015-7-1_17-3-58.png314 bytes · Views: 551 -
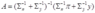 upload_2015-7-1_17-3-58.png677 bytes · Views: 546
upload_2015-7-1_17-3-58.png677 bytes · Views: 546 -
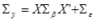 upload_2015-7-1_17-3-58.png481 bytes · Views: 506
upload_2015-7-1_17-3-58.png481 bytes · Views: 506 -
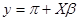 upload_2015-7-1_17-3-58.png440 bytes · Views: 529
upload_2015-7-1_17-3-58.png440 bytes · Views: 529 -
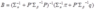 upload_2015-7-1_17-3-58.png786 bytes · Views: 530
upload_2015-7-1_17-3-58.png786 bytes · Views: 530 -
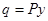 upload_2015-7-1_17-3-58.png337 bytes · Views: 539
upload_2015-7-1_17-3-58.png337 bytes · Views: 539