Proving Snell's law using Euler-Lagrange equations

[CGandC]

Homework Statement

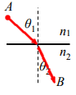
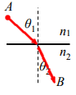
Prove that snell's law ${n_1}*{sin(\theta_1)} ={n_2}*{sin(\theta_2)}$ is derived from using euler-lagrange equations for the time functionals that describe the light's propagation, As described in the picture below.

Given data:
the light travels in two mediums , one is $n_1$ and the other is $n_2$
The speed of the light in these mediums are:
$v_1=\frac{c}{n_1}$ and $v_2=\frac{c}{n_2}$ respectively
and the angles of incident and refraction are: $\theta_1$ and $\theta_2$ respectivley

Homework Equations

$\frac{d}{dt} \left ( \frac{\partial L}{\partial \dot q} \right ) - \frac{\partial L}{\partial q}=0$
$distance = speed*time$ ,$t_0 = 0$ and the velocity is constant
$Arclength = ds = \sqrt{dx^2+dy^2}$

The Attempt at a Solution

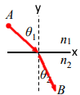
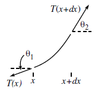
I'll look at medium $n_1$ : I'll look at an infinitesimal piece of the arclength of the light:

and using the distance formula
${v_1*dt}={\sqrt {( x-(x+dx) )^2+( y-(y+dy) )^2} }={\sqrt{( dx) )^2+( dy) )^2}}={\sqrt {1+\frac{dy}{dx}^2} }*dx$
so: $t = \int \frac{ds}{v_1}=\int \frac{\sqrt{dx^2+dy^2}}{v_1}=\int \frac{\sqrt{1+y'^2}}{v_1}dx$

Using euler lagrange equations, I find that $y$ is a cyclical coordinate, therefore:
$\frac{d}{dx} \left ( \frac{y'}{v_1*\sqrt {1+(y')^2}} \right )=0$
so: $\frac{y'}{v_1*\sqrt {1+(y')^2}} =const$ and re-arranging:
$\frac{dy}{v_1*\sqrt{dx^2+dy^2}} = const$
knowing that ( from the pictures) : $\frac{dy}{\sqrt{dx^2+dy^2}}=\frac{dy}{ds} =cos(\theta_1)$ and that
$v_1=\frac{c}{n_1}$ then I can re-write $\frac{dy}{v_1*\sqrt{dx^2+dy^2}} = const$ as:
${n_1}*{cos(\theta_1)}/c = const$
Using similar methodology with the second medium, I get: ${n_2}*{cos(\theta_2)}/c = const$
I notice that there is a conserved quantity from the euler-lagrange equations, therefore:
${n_1}*{cos(\theta_1)} ={n_2}*{cos(\theta_2)}$

So here's the problematic point , I got : ${n_1}*{cos(\theta_1)} ={n_2}*{cos(\theta_2)}$ instead of : ${n_1}*{sin(\theta_1)} ={n_2}*{sin(\theta_2)}$
What seems to be the problem? is it my understanding of what I'm doing with the euler-lagrange equation?

 

[Orodruin]

Using euler lagrange equations, I find that y is a cyclical coordinate

This is not correct as $v$ depends on $y$.

Edit: Because of this reason, it is easier if you turn your setup 90 degrees and make the interface between the media a line of constant $x$ instead of constant $y$. Then your integrand will not depend on $y$ as the refractive index will depend on $x$ only.

Alternatively, you can use that the integrand you wrote down does not depend explicitly on $x$ and use the Beltrami identity, but this is a longer computation.

 

[CGandC]

This is not correct as $v$ depends on $y$.

Edit: Because of this reason, it is easier if you turn your setup 90 degrees and make the interface between the media a line of constant $x$ instead of constant $y$. Then your integrand will not depend on $y$ as the refractive index will depend on $x$ only.

Alternatively, you can use that the integrand you wrote down does not depend explicitly on $x$ and use the Beltrami identity, but this is a longer computation.

Using Beltrami identity:

I get the correct answer.
However, can you please elaborate on why $v$ depends on $y$? because I know from the given data that $v_1 = const = c/n_1$

 

[Orodruin]

Using Beltrami identity:

I get the correct answer.
However, can you please elaborate on why $v$ depends on $y$? because I know from the given data that $v_1 = const = c/n_1$

You cannot just consider one of the regions. Your $v$ is the speed of light as a function of position and since you have two different media, it depends on position. In this orientation, the media are oriented in such a way that $v$ depends only on $y$. You are also particularly interested in the crossing of the boundaries of the media, i.e., when you move from one medium to the other. It should be pretty clear that the refractive index changes as a function of $y$ at this point.

 

[Orodruin]

To be more specific, if you consider just one medium, what you get out is indeed $n \cos(\theta) = C$, where $C$ is some constant. This tells you that the direction within the medium is constant, but it tells you nothing about the relation between the angles in the different media. In particular, if you want to consider the transition, you need to consider a section where $n$ depends explicitly on $y$.

 

[CGandC]

I think I understand, you are saying that $v$ is basically a heaviside function ( which depends on y ) as follows:
$v = \begin{cases} v_1 & 0 \leq y, \\ v_2 & y < 0. \end{cases}$

And for this reason, I have to use Beltrami Identity, as $v$ depends on $y$.

 

[Orodruin]

Yes.

 

[CGandC]

Yes.

Looking into the case further, my functional for the problem is :$t = \begin{cases} \int \frac{ds}{v_1} & 0 \leq y, \\ \int \frac{ds}{v_2} & y < 0. \end{cases}$

$Arclength = ds = \sqrt{dx^2+dy^2}$

So looking at the functional, we see that it depends on $y'$ and $y$ ( depends on y because the value of the function in the integral is different for different y's)
and for this reason, I conclude that I must use Beltrami's identity when solving for each interval of $y$ . and I'll get eventually:
${n_2}*{sin(\theta_2)} = const$ and ${n_1}*{sin(\theta_1)} = const$
Do you agree?

However, I have another question which bugged me - these constants are called ' conserved quantities ' , I don't understand why are they equal? ( I.e : ${n_1}*{sin(\theta_1)}= {n_2}*{sin(\theta_2)}$ ) , after all, I used euler-lagrange/Beltrami identity for different $y$ intervals ,then the constant that arises must be different for each equation also.

 

[Orodruin]

Looking into the case further, my functional for the problem is :$t = \begin{cases} \int \frac{ds}{v_1} & 0 \leq y, \\ \int \frac{ds}{v_2} & y < 0. \end{cases}$

$Arclength = ds = \sqrt{dx^2+dy^2}$

So looking at the functional, we see that it depends on $y'$ and $y$ ( depends on y because the value of the function in the integral is different for different y's)
and for this reason, I conclude that I must use Beltrami's identity when solving for each interval of $y$ . and I'll get eventually:
${n_2}*{sin(\theta_2)} = const$ and ${n_1}*{sin(\theta_1)} = const$
Do you agree?

Essentially, but I would not write what you wrote for $t$. It is more instructive and less prone to errors to write it as
$$
ct = \int n\, ds,
$$
where $n = n(y(x)) = n_1 + (n_2-n_1)\theta(-y(x))$, where $\theta$ is the Heaviside function. You do not have a separate EL equation for each medium, your integrand is $n(y(x)) \sqrt{1 + y'(x)^2}$ and this gives you a constant of motion which is $n(y) \sin(\theta)$.

However, I have another question which bugged me - these constants are called ' conserved quantities ' , I don't understand why are they equal? ( I.e : ${n_1}*{sin(\theta_1)}= {n_2}*{sin(\theta_2)}$ ) , after all, I used euler-lagrange/Beltrami identity for different $y$ intervals ,then the constant that arises must be different for each equation also.

You do not have two separate differential equations. You have one differential equation where one of the functions that it depends on depends on the value of $y$.

 

[CGandC]

Essentially, but I would not write what you wrote for $t$. It is more instructive and less prone to errors to
$$
ct = \int n\, ds,
$$
.

Thinking about it, I don't think the 'ds' is the same for the two mediums , i'll give you an analogy:

Suppose there is a wire and I look at an infinitesimal part of it, it will have different tensions on each end - making different angles with respect to the horizontal line:

Therefore:
$cos(\theta_1)=\frac{dx}{ds_1\vert_{x}^{} } = \frac{dx}{\sqrt{dx^2+dy^2\vert_{x}^{}} } = \frac{1}{\sqrt{1+(\frac{dy}{dx})^2 \vert_{x}^{}} }$
$cos(\theta_2)=\frac{dx}{ds_2\vert_{x+dx}^{} } = \frac{dx}{\sqrt{dx^2+dy^2\vert_{x+dx}^{}} } = \frac{1}{\sqrt{1+(\frac{dy}{dx})^2 \vert_{x+dx}^{}} }$

So it appears that there are different arc lengths,therefore,I think the integral cannot be written as: $ct = \int n\, ds,$
since $ds_1 \neq ds_2$

Note: the problem above with the wire is not related to the snell's law problem , it was just given as an analogy to a difficulty

 

[Orodruin]

Thinking about it, I don't think the 'ds' is the same for the two mediums , i'll give you an analogy:

Suppose there is a wire and I look at an infinitesimal part of it, it will have different tensions on each end - making different angles with respect to the horizontal line:
View attachment 220769

Therefore:
$cos(\theta_1)=\frac{dx}{ds_1\vert_{x}^{} } = \frac{dx}{\sqrt{dx^2+dy^2\vert_{x}^{}} } = \frac{1}{\sqrt{1+(\frac{dy}{dx})^2 \vert_{x}^{}} }$
$cos(\theta_2)=\frac{dx}{ds_2\vert_{x+dx}^{} } = \frac{dx}{\sqrt{dx^2+dy^2\vert_{x+dx}^{}} } = \frac{1}{\sqrt{1+(\frac{dy}{dx})^2 \vert_{x+dx}^{}} }$

So it appears that there are different arc lengths,therefore,I think the integral cannot be written as: $ct = \int n\, ds,$
since $ds_1 \neq ds_2$

Note: the problem above with the wire is not related to the snell's law problem , it was just given as an analogy to a difficulty

No, this is wrong.

Obviously the value of $\sqrt{1+y'(x)^2}$ will change along a curve unless $y(x)$ is a straight line, but the functional expression for $ds$ will not, i.e., $ds = \sqrt{1+y'(x)^2}\, dx$.

 

[CGandC]

but If for example, in medium 1 : $y'(x) = -x$ and in medium 2 : $y'(x) = -2x$
then
$ds_1 = \sqrt{1+(-x)^2}\, dx \neq ds_2 = \sqrt{1+(-2x)^2}\, dx$
so this means there is a separate functional expression for each medium.

 

[Orodruin]

but If for example, in medium 1 : $y'(x) = -x$ and in medium 2 : $y'(x) = -2x$
then
$ds_1 = \sqrt{1+(-x)^2}\, dx \neq ds_2 = \sqrt{1+(-2x)^2}\, dx$
so this means there is a separate functional expression for each medium.

No, this is a bad idea. You are searching for the function $y(x)$ so you cannot just assume that it takes some form. Then, based on what you find, you can compute the angle. You are looking at the functional form in terms of a function of $x$, $y(x)$, and $y'(x)$, which should be treated as independent parameters of the integrand.

 

[Ray Vickson]

but If for example, in medium 1 : $y'(x) = -x$ and in medium 2 : $y'(x) = -2x$
then
$ds_1 = \sqrt{1+(-x)^2}\, dx \neq ds_2 = \sqrt{1+(-2x)^2}\, dx$
so this means there is a separate functional expression for each medium.

Not really; the arc-length expression is $ds = \sqrt{1 + y'^2(x)} \: dx$ in both regions, but the function $y'$ has a piecewise definition:
$$y'(x) = \begin{cases} -x, & x \in \text{Region 1} \\
-2x, & x \in \text{Region 2}
\end{cases}
$$

 

[CGandC]

So compiling what I've learned from the above:
$dt = \int{ \frac{ds}{v_1} } + \int{ \frac{ds}{v_2} } = \int{ \frac{\sqrt{1+y'^2}dx}{v_1} } +\int{ \frac{\sqrt{1+y'^2}dx}{v_2} }= \int{ \frac{ds}{v} } =\int{ \frac{\sqrt{1+y'^2}dx}{v} }$
where: $y'(x) = \begin{cases} A(x), & y < 0 \\ B(x), & y > 0 \end{cases}$
and: $v = \begin{cases} v_1, & y < 0 \\ v_2, & y > 0 \end{cases}$
and eventually solving $\int{ \frac{\sqrt{1+y'^2}dx}{v} }$ using Beltrami identity, I get the right answer.

I have another question arising from the above - If have a functional ,then It must be dependant on one integral and not more in order for me to use Euler-lagrange/Beltrami equations for it, otherwise, why you worked so hard to join each separate integral into one integral?
for example :
instead of having $h[f(x),g(x)] = \int{f(x)dx} + \int{g(x)dx}$ , I need to find some way to join the integrals together to form something like:
$h[f(x),g(x)] = \int{(f(x)+g(x))dx}$
And I do this in order for me to be able to use Euler-lagrange/Beltrami equations for the functional. Is my assumption correct?
Asking the question in another way : I can use Euler-Lagrange/Beltrami equations only for a functional which depends on only one integral?

 

[Orodruin]

where: $y'(x) = \begin{cases} A(x), & y < 0 \\ B(x), & y > 0 \end{cases}$

You really should not do this to yourself because it is blocking your understanding. The entire point is that $y(x)$ is an unknown function. It may have any form, but the question you are asking is ”what form will be a stationary function of the functional?”. As such, you should a priori not assume anything about $y(x)$ or its derivative. The functional you write down is a map from a set of functions to real numbers that describes the time it would take to travel along the path it describes with some predetermined velocity $v(x,y)$.

Regarding your second question you seem to be asking what happens when your functional depends on two functions rather than when you have two integrals. Much like in regular calculus where a multivariable function must have all partial derivatives equal to zero, you get one EL equation per function that your functional depends on. This should be discussed in any basic textbook that covers variational calculus. I would suggest one, but I am biased.