chris99191
- 9
- 0
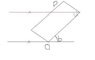
1. For the diagram in the attachment, prove that the height of P above floor after being tilted is h(cosb+2sinb)
2. h(cosb+2sinb)
3. I think you need to divide them up into triangles and then use the angles for each as well as maybe using a sums to products formula
2. h(cosb+2sinb)
3. I think you need to divide them up into triangles and then use the angles for each as well as maybe using a sums to products formula