Law91
- 8
- 0
Hi,
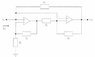
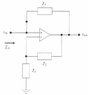
i have this gyrator circuit that is equivalent to an inductor of 11.11mH and I am required to show that if the opamps are ideal and assuming that the circuit is stable that
Zin = (Z1*Z3*Z5) / (Z2*Z4)
ive got for an ideal opamp that i+ = i- = 0 and that Aol = infinity
the ciruit is posted below..
any assistance would be greatly appreciated in proving Zin
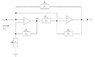
i have this gyrator circuit that is equivalent to an inductor of 11.11mH and I am required to show that if the opamps are ideal and assuming that the circuit is stable that
Zin = (Z1*Z3*Z5) / (Z2*Z4)
ive got for an ideal opamp that i+ = i- = 0 and that Aol = infinity
the ciruit is posted below..
any assistance would be greatly appreciated in proving Zin