Oatmeal11
- 6
- 0
Homework Statement
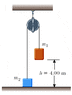
Two masses are connected by a light string passing over a light, frictionless pulley as in the figure below. The m1 = 5.30 kg object is released from rest at a point 4.00 m above the floor, where the m2 = 2.85 kg object rests.
a) Determine the speed of each object when the two pass each other.
b) Determine the speed of each object the moment the 5.3 kg mass hits the floor.
c) How much higher does the 2.85 kg mass travel after the 5.3 kg mass hits the floor?
Homework Equations
KE=(1/2)mv^2
F=ma
y=vot+.5at^2
The Attempt at a Solution
I treated it as one system and made a free body diagram. I inserted it into the equations, sum of F=ma and added up force of tension on string +force of gravitiy=a(m1+m2) I solved for acceleration then inserted that into the v^2=vo^2+2ax. Unfortunately the answers are all wrong and I'm not even sure i started this problem rigiht. Helpl??