Pulley's mass is invariant to the physics problem?

[Helena Wells]

I have this system of masses and the goal is to find the velocity of $m_1$ at the ground. But it gives me the moment of inertia of the pulley as well which is $xMR^2$.

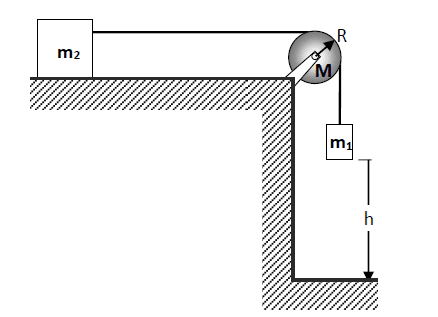I know how to solve a pulley problem but since it gives me the moment of inertia of the pulley maybe it has something to do with the solution? and I don't know if I should use the normal method.Help appreciated!

 

[Doc Al]

What's "the normal method"? Often in these sorts of problems, the pulley is given as massless but that is not the case here.

Start (in the usual manner ) by drawing free body diagrams for both masses and the pulley.

 

[Helena Wells]

Hmm the 'normal method' is we treat m1 and m2 as 1 object m = m1+m2.

Then we apply Newton's second law of motion ΣF = ma where the forces sign depends on if it resists or not the motion of m in our case weight m2 - friction . And since we know the acceleration we can find time of fall and velocity at the ground.Then we apply Newton's 2nd law again for each object m1 and m2 with our found acceleration to find the tension of the rope in both objects.

But all the examples I have done this don't give mass to the pulley so I was wondering if anything could change here

 

[Doc Al]

Hmm the 'normal method' is we treat m1 and m2 as 1 object m = m1+m2.

That won't help here, since the pulley has mass also. (Even for the massless pulley case, I don't like that method.)

What I recommend is to apply Newton's 2nd law to each object. That will give you three equations and three unknowns, which you can solve. As usual, you'll solve for the acceleration and then do your kinematic analysis.

 

[PeroK]

Hmm the 'normal method' is we treat m1 and m2 as 1 object m = m1+m2.

Then we apply Newton's second law of motion ΣF = ma where the forces sign depends on if it resists or not the motion of m in our case weight m2 - friction . And since we know the acceleration we can find time of fall and velocity at the ground.Then we apply Newton's 2nd law again for each object m1 and m2 with our found acceleration to find the tension of the rope in both objects.

But all the examples I have done this don't give mass to the pulley so I was wondering if anything could change here

I suspect this is one of those problems that requires you to think for yourself! What do you know about rotational motion? What do you know about energy?

 

[Helena Wells]

Hello its herperfectbornimoutlook here. This is my main account I had forgot it existed! Anyway I was thinking about applying Netwon's 2nd law of motion (torque) for the pulley but I don't think it will help me much.And how could conservation of energy help me here?

 

[Doc Al]

As @PeroK hints, there are several ways of solving this one. (Well, at least two.) I suggested one way since it uses Newton's 2nd law (which I assume you know). But there's an even easier way if you've gotten far enough in your studies.

 

[Doc Al]

Anyway I was thinking about applying Netwon's 2nd law of motion (torque) for the pulley but I don't think it will help me much.

Try it and see!

And how could conservation of energy help me here?

Well, is energy conserved?

 

[A.T.]

Anyway I was thinking about applying Netwon's 2nd law of motion (torque) for the pulley but I don't think it will help me much.

That's exactly what you were given the moment of inertia for.

 

[haruspex]

You are meant to assume the string does not slip on the pulley. Think what that means for the tensions in different sections of the string. (Or use energy, which avoids having to worry about forces.)

 

[Lnewqban]

... I know how to solve a pulley problem but since it gives me the moment of inertia of the pulley maybe it has something to do with the solution?

As the string does not slip on the pulley, its rotational inertia slows down any linear movement of the string-m1-m2 system.
Using all your strength, you will never be able to open a very heavy door as quickly as you could open a light door.

Copied from
https://en.m.wikipedia.org/wiki/Moment_of_inertia

"When a body is free to rotate around an axis, torque must be applied to change its angular momentum. The amount of torque needed to cause any given angular acceleration (the rate of change in angular velocity) is proportional to the moment of inertia of the body."

 

[hutchphd]

1. Make a labelled drawing. Because the pulley has mass you cannot assume the Tension in the horizontal string $T_1$ is equal to the vertical string segment $T_2$
2. You have three unknown quantities $T_1,T_2, a$ where a is the acceleration of, say, $m_1$
3. You have three equations from Newton two linear (masses) and one rotational (pulley). Make a free body diagram for each and write down the equations
4. Solve

 

[wrobel]

another problem for the law of energy conservation

 

[hutchphd]

That, too. Or do it both ways for fun/pedagogy!