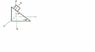Pushing an incline so mass on ramp accelerates upward

[matineesuxxx]

This seems to be a slight variation of a pretty standard problem, however I didn't have any luck finding any seemingly helpful information. I am mainly wondering if I am not getting the FBDs correct?

Homework Statement

A block of mass m is sitting on a movable ramp of mass M with an incline of \theta degrees to the horizontal. The system is initially held at rest. Once released, a force, F, pushes the vertical side of the ramp such that the block accelerates upward along the incline. There is no friction anywhere; Write an expression for the force.

Homework Equations

\sum \text{F} = ma

The Attempt at a Solution

The FBD's are in the attached image.

I seem to be arriving at a system with one more variable than equations, so I am definitely not understanding something, and I believe it has to do with the FBD? Here is what I come up with:

As the inclines acceleration (a_{\text{I}}) is purely on the horizontal plane, then the components of the blocks acceleration (a_B) are:

a_x = a_{\text{B}}\cos \theta - a_{\text{I}} and a_y = a_{\text{B}}\sin \theta.

for the little mass, m:

\sum \text{F}_x = N_1 \sin \theta = m(a_{\text{B}} \cos \theta - a_{\text{I}})

\sum \text{F}_y = N_1 \cos \theta - mg = ma_{\text{B}}\sin \theta

and for the incline:

\sum \text{F}_x = \text{F} - N_1\cos \theta = a_{\text{I}}M
I'm pretty stuck and have no idea what it is that I'm missing, so I would really appreciate it if someone could give me a hint.

 

[matineesuxxx]

Forgot to include the FBD.

[edit] The rightmost FBD is for the incline.

 

[BiGyElLoWhAt]

Is the ramp moving vertically or is it rotating via the external force?

Take a ping pong ball and put it on a board. Angle it and, keeping the angle the same, move the whole system upwards. What happens?

Now, same situation, but hold the board by one end and swing it up over your head (you might want to be outside) what happens?

 

[matineesuxxx]

Is the ramp moving vertically or is it rotating via the external force?

Take a ping pong ball and put it on a board. Angle it and, keeping the angle the same, move the whole system upwards. What happens?

Now, same situation, but hold the board by one end and swing it up over your head (you might want to be outside) what happens?

I think that I may have stated the problem in an unclear way. So the incline is resting on the ground and the force is pushing it along the horizontal and there is no rotation in the ramp. I want to find an expression for the magnitude of the force so that the block slides up the ramp leftward as the ramp slides to the right.

 

[BiGyElLoWhAt]

Oh, ok. I thought the ramp was moving upward, not rightward. So initially, you can just look at the acceleration of the ramp, and see what conditions need to be met in order for the block to move upward.

Can you tell me what these are? Basically you have force of Earth on block and force of ramp on block.

Hint* think components or rotate your axes.

 

[BiGyElLoWhAt]

Maybe a better question would be which way should the net force be directed?

 

[Doc Al]

Are you trying to find the minimum value of F to accelerate the mass up the incline?

 

[matineesuxxx]

Maybe a better question would be which way should the net force be directed?

Well, if I draw the acceleration vectors for the block and the incline - the block with respect to the incline is up and to the left and the incline with respect to the ground is only to the right - then the resulting acceleration vector for the block with respect to the ground is up and to the right. That would then be the direction of the net force, no?

Are you trying to find the minimum value of F to accelerate the mass up the incline?

yes, I am.

 

[Doc Al]

yes, I am.

Good. And that was my hint.

 

[matineesuxxx]

Good. And that was my hint.

Ah, ok. Well, my first attempt at this problem was to find the maximum force with which to push the incline such that the block stays still, since any force greater than that would cause the block to accelerate upward, but I am actually thinking that its not the way I should go

 

[Doc Al]

Ah, ok. Well, my first attempt at this problem was to find the maximum force with which to push the incline such that the block stays still, since any force greater than that would cause the block to accelerate upward, but I am actually thinking that its not the way I should go

I would say that finding the force that would cause the block to have no vertical acceleration is the way to go.

Did you find that force?

 

[matineesuxxx]

I would say that finding the force that would cause the block to have no vertical acceleration is the way to go.

Did you find that force?

I did, and here is what I got:

\text{F} = g(m+M)\frac{\sin \theta - \mu_{s} \cos \theta}{\cos \theta + \mu_{s} \sin \theta}.

My logical check was that if \mu_{s} = 0 then \text{F} = g(m+M)\tan \theta which is what I got when I solved the no friction situation.

for \mu_{s} \neq 0 and if we let \theta = 0 then we can view the system as two rectangular blocks stacked together and i get $$\text{F} = g(m+M)\mu_{s}$$ which is also what i got when i solved that situation seperatly.

Finally, if \mu_{s} = 0 and \theta=0 then we have the two block situation again, but no friction, so there is no way you can push the bottom block so that the top block has no acceleration with respect to the bottom block, which is what i get from that equation as well, \text{F} = 0.Is that correct?

 

[BiGyElLoWhAt]

I did, and here is what I got:

\text{F} = g(m+M)\frac{\sin \theta - \mu_{s} \cos \theta}{\cos \theta + \mu_{s} \sin \theta}.
Is that correct?

That's not quite what I'm getting, but we might be starting from 2 different places and getting to 2 different solutions. How did you start?

My N2L is $\Sigma \vec{F} = m \vec{a} = \vec{N} + \vec{w} = (mg + \frac{m}{M}F_{on ramp})<cos( \theta), sin( \theta)> + mg<cos( \theta), -sin(\theta)>$

do you see where I got everything? The $\frac{m}{M}F_{onramp}$ is the force on the ramp, divided by the mass of the ramp (the acceleration on the ramp) and since the block isn't moving wrt the ramp (solving for the force needed to keep the change in height 0) the system moves as one, so the acceleration of the ramp will be the acceleration of the block. The force is then $m\vec{a}_{oframp}$

 

[BiGyElLoWhAt]

What your equation looks like is you're treating the F on ramp as a force on the system, not just the ramp. (M+m)g

 

[Doc Al]

I did, and here is what I got:

\text{F} = g(m+M)\frac{\sin \theta - \mu_{s} \cos \theta}{\cos \theta + \mu_{s} \sin \theta}.

Yes, that's good. (If you get rid of the friction! Why complicate things with friction?)

 

[Doc Al]

What your equation looks like is you're treating the F on ramp as a force on the system, not just the ramp.

F is both: It acts on the ramp and on the "ramp + block" system.

 

[matineesuxxx]

That's not quite what I'm getting, but we might be starting from 2 different places and getting to 2 different solutions. How did you start?

If we are finding the maximum force with which to push the incline so the block has no vertical acceleration, then the block/ramp system is one mass with only one acceleration in the positive x direction, so i get \text{F}=m_Ta = (m+M) a \implies a = \text{F}/(m+M). So now we only need consider the forces on the block,
$$\sum \text{F}_x = N(\sin \theta - \mu_s \cos \theta) = ma\;\;\;\;\;\;\;\;\;\;\;\;(1)$$
$$\sum \text{F}_y = N(\cos \theta + \mu_s \sin \theta) - mg = 0 \;\;\;(2)$$

so dividing (1) by (2) and substituting in a, I get my answer.

Yes, that's good. (If you get rid of the friction! Why complicate things with friction?)

Who likes friction, eh? ;)

 

[matineesuxxx]

Yes, that's good. (If you get rid of the friction! Why complicate things with friction?)

Also, the reason I thought I shouldn't tackle it in this way was because the answer the book provides is $$\text{F} = \mu_{\text{k}}(m+M)g\sin \theta \cos \theta $$, but now that I think about it, their answer says if there is no friction in the system then a force of 0 N will cause the block to accelerate up the ramp. what??

 

[Doc Al]

What book are you using?

 

[matineesuxxx]

What book are you using?

Physics for Scientists and Engineers An Interactive Approach by Nelson.

One of the profs at the university I go to co-authored the book, so we used it in the advanced physics class. Dropped it after two days, so I'm trying to get ahead of the game before I take it again in the fall.

 

[SammyS]

My suggestion for solving this problem is to find the force, F, necessary so the block doesn't move up or down the ramp, i.e. the vertical component of the block's acceleration is zero. (Yes, this was you initial strategy.)

There's no need to consider friction at all.https://www.physicsforums.com/attachment.php?attachmentid=70913&d=1403804470

 

[Doc Al]

My suggestion for solving this problem is to find the force, F, necessary so the block doesn't move up or down the ramp, i.e. the vertical component of the block's acceleration is zero. (Yes, this was you initial strategy.)

There's no need to consider friction at all.

Exactly. (Which is what I have suggested above.) Makes it much easier if you don't have to bother with friction.