- #1
ramdas
- 79
- 0
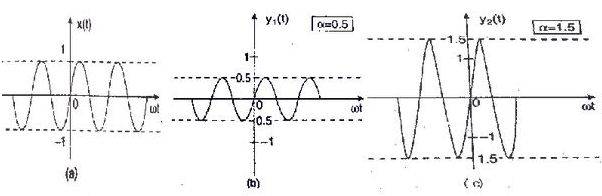
Suppose 3 1D Signals x(t), y1(t) and y2(t) are given as
x(t)=sin(40*pi*t);
y1(t)=.5*sin(40*pi*t) and
y2(t)=x(t)+y1(t).
Left side =Right side
Here,values of x(t)and y1(t)i.e.(Right side) are given and we get y2(t)(Left side).The plots of x(t),y1(t) and y2(t)
are plotted below
Now,in the next case,suppose left side is given and we are to asked to find right side.But the twist is that here signal not 1D .It is 2D i.e an image! shown below

I know that image consists ofsummation of thousand of signals but here I want to see plots of only 4 to 5 signals from the image (like of x(t) and y1(t) shown above) but not the whole spectrum. How it can be done?
x(t)=sin(40*pi*t);
y1(t)=.5*sin(40*pi*t) and
y2(t)=x(t)+y1(t).
Left side =Right side
Here,values of x(t)and y1(t)i.e.(Right side) are given and we get y2(t)(Left side).The plots of x(t),y1(t) and y2(t)
are plotted below
Now,in the next case,suppose left side is given and we are to asked to find right side.But the twist is that here signal not 1D .It is 2D i.e an image! shown below
I know that image consists ofsummation of thousand of signals but here I want to see plots of only 4 to 5 signals from the image (like of x(t) and y1(t) shown above) but not the whole spectrum. How it can be done?