Alexanddros81
- 177
- 4
Homework Statement
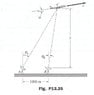
the plane C is being tracked by radar stations A and B. At the instant shown,
the triangle ABC lies in the vertical plane, and the radar readings are θA=30o,
θB = 22o, θA(dot) = 0.026rad/s and θΒ(dot) = 0.032rad/s. Determine (a) the altitude y; (b) the speed v; and (c) the climb angle α of the plane at this instant
Homework Equations
The Attempt at a Solution
I guess I can find (a) from trogonometry. Any hints for part (b)?