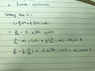QM Weinberg Probl 9.1: Solving for Eq of Motion with Defined Lagrangian

[Kyueong-Hwang]

Homework Statement

specific lagrangian is defined.
Have to get a equation of motion

Homework Equations

[/B]
Lagrangian is defined as

The Attempt at a Solution

[/B]

eq of motion that i drive like

i guess term of f(x) have to vanish or form a shape of curl.
but it didn't be clear.
May i did something wrong but i can't catch that...

 

[BvU]

Hello Kyueong-Hwang,

I find it hard to read what you write after | )
You want $\partial {\mathcal L}\over \partial x_i$ so I expect to see a $\partial x_i$ in the denominator, not $\partial x_i \; f(\vec x)$ ?

Time to learn some $\LaTeX$ (item 7 here) !

 

[Kyueong-Hwang]

$$ \frac {\partial \mathfrak {L}} {\partial x_i} =\frac {\partial \vec x} {\partial t} \cdot \partial x_i \vec f \left(\vec x \right) - \partial x_i V \left(\vec x \right)$$
$$ \frac {\partial} {\partial t} \left(\frac {\partial \mathfrak {L}} {\frac {\partial x_i} {\partial t}} \right)= m \ddot x_i + \vec \nabla f_i \left(\vec x \right) \cdot \frac {\partial \vec x} {\partial t}$$

I thought $\LaTeX$ is hard to do.
But its quite fun XD

so. with these eqs we can make euler-lagrangian, eq of motion.
I guess changing index i in $x_i$ to $\vec x$ yield that vanish or assemble terms of $f \left(\vec x \right)$

 

[Kyueong-Hwang]

if $x_i$ is a axis of 3-dim cartesian coordinate two $f \left( \vec x \right)$ terms yield $\vec \nabla \times \vec f \left(\vec x \right)$
But there is no such statement assure that $x_i$ is 3-dim cartesian coordinate.

And someone in this forum site says in higher than 3 dimension curl is hard to define.
also on wiki only 3, 7 dimension define curl

 

[BvU]

$$\frac {\partial \mathfrak {L}} {\partial x_i} =\dot{ \vec x_i} {\partial f_i \left(\vec x \right)\over \partial x_i } - {\partial V \left(\vec x \right)\over \partial x_i }$$
don't write$$
\frac {\partial} {\partial t} \left(\frac {\partial \mathfrak {L}} {\frac {\partial x_i} {\partial t}} \right)$$for two reasons: 1. it is $d\over dt$, not $\partial\over \partial t$, and 2. this way you will mix up $x_i$ and $\dot x_i$ -- they should be treated as independent variables !

So $$
\frac {\partial \mathfrak {L}} {\partial \dot x_i} = m\dot x_i + \vec f_i(\vec x)$$

 

[BvU]

if $x_i$ is a axis of 3-dim cartesian coordinate two $f \left( \vec x \right)$ terms yield $\vec \nabla \times \vec f \left(\vec x \right)$

Curl doesn't appear here.

 

[Kyueong-Hwang]

alright thanks
1, at latex q&a page i miss d notation so i use partial
2. \dot \vec x isn't work so i think x_i does too

 

[Kyueong-Hwang]

ah
your right. my fault.

is there any way to make this eq more clear?
next question is to make hamiltonian and find Schrodinger eq.
It may should be more clear.

 

[BvU]

is there any way to make this eq more clear?

Well, if $\vec f(\vec x)$ is time independent, you get $m\ddot x = ...$

Re Schr eq:
Please post a clear and complete problem description. For a different exercise, start a different thread.