- #1
moriheru
- 273
- 17
My question concerns a really simple differential equation for the zeroth wavefunction of a harmonic oscillator.
I have pretty much got it but my solution just differs by a constant,so I thought why think when one can ask other people :). Here is the equation:
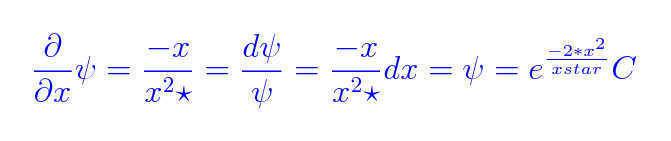
Where the x star represent a variable involving mass frequency and Plancks constant. There is a psi function missing in the second equation (for any latex tips please e-mail me)
(Posted to early so there was no equation on the original post;had to edit it)
I have pretty much got it but my solution just differs by a constant,so I thought why think when one can ask other people :). Here is the equation:
Where the x star represent a variable involving mass frequency and Plancks constant. There is a psi function missing in the second equation (for any latex tips please e-mail me)
(Posted to early so there was no equation on the original post;had to edit it)
Last edited: