Quantum Mechanics - Question about the Finite Square Well

[rachelph]

Hi,

I'm preparing for an exam, and I'm going over past papers. I've solved parts a & b of this question without any problems, however I'm finding it hard to understand part c.

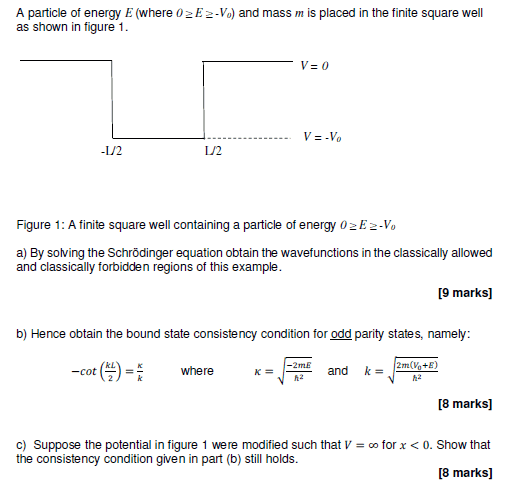
I thought of shifting the boundary conditions so I'd have 0 and L in the place of ± L/2, but that would not work because the boundary condition to solve the consistency condition requires x = L/2.
Could I get some pointers on where to start? I'm incredibly lost.

 

[Dr Transport]

if V = 0 for x < 0 think about where the nodes of the wave function are for an infinite well...

 

[rachelph]

if V = 0 for x < 0 think about where the nodes of the wave function are for an infinite well...

Between x = 0 and x = L/2?

 

[Dr Transport]

draw the wave functions for an infinite well, where does the central node cross the energy line??

 

[rachelph]

draw the wave functions for an infinite well, where does the central node cross the energy line??

Alright, I think I have finally figured out the question.

So, before, I had V = 0 for x < -L/2, V = 0 for x > L/2, and V = -Vo for -L/2 < x < L/2.

If the potential is modified such that x < 0 is V = ∞. I'd still have V = -Vo for 0 < x < L/2. and V = 0 for x > L/2
This means that the wavefunction for region 3 (x > L/2) would still hold the same as in part b, and for 0 < x < L/2 the wavefunction would be the same as in the classically allowed region as in part b. So when I apply the boundary condition at x = L/2 I'm going to get the same consistency condition seen in part b, as required.