Qubit Math: Partitioning Phi into BetaA and BetaB

[Elroy]

Hi All,

I'm gradually teaching myself quantum computing, being an excellent programmer and fair at linear algebra and geometry.

To learn it, I'm writing a quantum computer emulator (complete with graphical representations). I'll share it when I get to some level of completion. The following is a screenshot of one piece of the program:

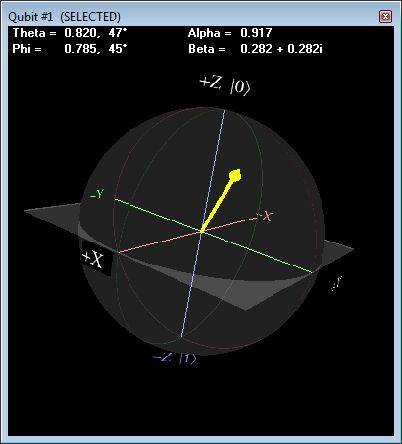
But here's why I'm posting. I'm struggling somewhat with the math needed to partition Phi into BetaA (real part) and BetaB (imaginary part). I'm trying to write a function with input of Theta and Phi (polar coordinates for qubit), and have it output Alpha, BetaA, and BetaB. As we know...
|Alpha|² + |Beta|² must = 1
...or, recognizing that Alpha doesn't need an imaginary part, we can simplify to...
Alpha² + |Beta|² = 1

...and Alpha is fairly easy to get from Theta. It's...

Temp1 = (Cos(Theta) + 1) / 2
Alpha = Sqrt(Temp1)

...so, since Temp1 is still squared, we can say that...
Temp2 = 1 - Temp1
...and then...
|Beta|² must = Temp2

However, now that Temp2 part must be partitioned between BetaA (the real part) and BetaB (the imaginary part). That's where I'm a bit stuck. To simplify things further, let's just stick with the first quadrant of the Phi Argand plane (the XY qubit plane). I can easily sort out the signs once I get past the BetaA and BetaB partitioning.

I can get VERY close just treating it as a linear relationship (before sqrt) to Phi, as follows (using Temp2 from above)...

BetaA = Sqrt(Temp2 * (1 - Phi / (PI/2)))
BetaB = Sqrt(Temp2 - BetaA²)

In fact, this works perfectly when Phi=0, Phi=PI/4, and Phi=PI/2.

However, it's not quite right when Phi isn't on a multiple of 45 degrees.

Some help with this BetaA and BetaB partitioning of Phi would be much appreciated.
Also, if anything isn't clear, please don't hesitate to ask, and I'll attempt to be more clear.

Regards,
Elroy

p.s. Just FYI, being the old curmudgeon that I am, this certainly isn't homework. With my PhD, I've been to school quite enough. :p

 

[Elroy]

Hmmm, well, I think I figured it out on my own.

I was just missing the Euler relation...

e^iφ = cos(φ) + i⋅sin(φ)

...which leads to...

β = cos(φ)⋅sin(θ/2) + i⋅sin(φ)⋅sin(θ/2)

...and also recognizing that, from my prior post...

sin(θ/2)² = Temp2

Therefore, cos(φ) and sin(φ) would seem to provide the partitioning I'm looking for. I've yet to try it but I have high hopes. My eyelids are heavy so it'll be tomorrow before I actually code it up.

 

[naima]

The easiest way to find $\beta = A+iB$ is to use the cartesian coordinates of your vector and the Pauli matrices.
You have $\rho = ( \alpha |0> + \beta |1>)(\overline \alpha <0| + \overline \beta <1|) = (Id + x \sigma_x + y\sigma_y + z\sigma_z )/2$
so $\alpha^2 = (1+z)/2$
and $\alpha \beta = A + iB = (x + iy)2$

This method is also valid inside the Bloch sphere.
the center of the sphere gives you the equiprobable mixture (|0><0| + |1><1|)2

 

[Elroy]

Thanks Naima,

I've implemented the β = cos(φ)⋅sin(θ/2) + i⋅sin(φ)⋅sin(θ/2) method and it seems to be working perfectly:
BetaA = cos(φ)⋅sin(θ/2)
BetaB = sin(φ)⋅sin(θ/2)

However, it's good to know how to handle qubits that might happen to be in mixed states.

Regards,
Elroy