DocZaius
- 365
- 11
Figure 2-4 in "Spacetime Physics" by Taylor & Wheeler
The figure illustrates the effects of free float on the perceived trajectory of a ball thrown in a room that is on a ledge and then in a room that is sawed free from the ledge.
In both cases, the ball is launched at the same speed and direction, and sprays ink on the side wall of the room. In all cases, the ball is thrown from right to left. Here is the illustration the book shows.
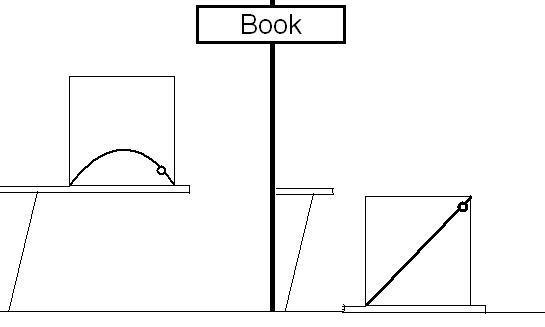
I have trouble with that illustration since it seems to me the ball would not make that ink trajectory in the free fall situation. To me it would seem to make this trajectory:
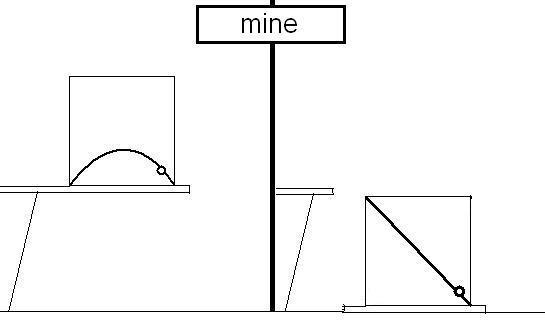
Can someone tell me why the book is right and I am wrong? To me it seems that once the ball is launched, it does not care if the house is free falling or not - it will arrive at the same spot relative to the stable side of the cliff. Why would it end up where the book says it does? Also, once the ball is launched in a free float situation, it seems it will behave as if having been launched int he same manner in the middle of space, and follow a straight line 45 degree angle trajectory to the opposite top corner of the room.
The figure illustrates the effects of free float on the perceived trajectory of a ball thrown in a room that is on a ledge and then in a room that is sawed free from the ledge.
In both cases, the ball is launched at the same speed and direction, and sprays ink on the side wall of the room. In all cases, the ball is thrown from right to left. Here is the illustration the book shows.
I have trouble with that illustration since it seems to me the ball would not make that ink trajectory in the free fall situation. To me it would seem to make this trajectory:
Can someone tell me why the book is right and I am wrong? To me it seems that once the ball is launched, it does not care if the house is free falling or not - it will arrive at the same spot relative to the stable side of the cliff. Why would it end up where the book says it does? Also, once the ball is launched in a free float situation, it seems it will behave as if having been launched int he same manner in the middle of space, and follow a straight line 45 degree angle trajectory to the opposite top corner of the room.
Last edited: