Question about basic Circuit, parallel and series connect

AI Thread Summary
R2 and R4 are neither in series nor in parallel according to the definitions provided. Series connections require components to be connected end to end, while parallel connections involve components connected to the same two nodes. The discussion clarifies that the configuration in question does not meet either criterion. Understanding these definitions is crucial for accurately analyzing circuit behavior. The conclusion emphasizes the importance of correctly identifying resistor arrangements in circuit analysis.
kougou
Messages
80
Reaction score
0

Homework Statement


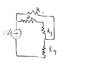
if I have something looks like the photo attach, could I say that
R2 and R4 are in series?

It asks to compute the current through the R2 branch, but I am curious about these two resistors are in series or not.



Homework Equations


definition of series and parallel connect.
Series: connecting end to end
Parallel: connecting to two same node


The Attempt at a Solution



No, they are not at all in parallel
 

Attachments

  • paint.jpg
    paint.jpg
    14.8 KB · Views: 439
Physics news on Phys.org
R2 and R4 are not in series and they are not parallel.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How to determine if electrical components are connected in parallel or in series?
Replies
10
Views
901
Finding parallel or in-series resistors
Replies
3
Views
667
Electrical Circuits - Parallel vs. Series
Replies
14
Views
1K
Why Do Capacitors Behave Differently in Series and Parallel Configurations?
Replies
20
Views
2K
Is This a Series or Parallel Circuit?
Replies
13
Views
897
Modification of Wheatstone Bridge
Replies
5
Views
1K
Current through an inductor as a function of time
Replies
10
Views
318
RCL series circuit analysis: Damping Constant
Replies
1
Views
635
Total equivalent resistance of a combined circuit
Replies
7
Views
2K
Solving series-parallel circuits
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top