tokki1510
- 2
- 0
In my pre-calculus textbook, the problem states:
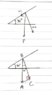
A 200-pound cart sits on a ramp inclined at 30 degrees. What force is required to keep the cart from rolling down the ramp?
The gravitational force can be represented by the vector F=0i-200j
In order to find the force we need to project vector F onto a unit vector in the direction of the ramp, so we use
v = cos(30°)i+(sin30°)j
After calculating the projection of F onto v, we get -100(cos(30°),(sin30°)). Taking the magnitude of this, we get that it takes a force of 100 pounds to keep the cart from rolling down the hill.
So I have a couple of questions about this.
First, why can we express force in pounds? Someone told me we can only express force in Newtons.
Second, I've seen others solve it this way:
The force required to keep the cart from rolling is 200×sin(30°)
And when they solve for the force perpendicular to the hill it is 200×cos(30°)
Why is it possible to calculate it this way as well?
A 200-pound cart sits on a ramp inclined at 30 degrees. What force is required to keep the cart from rolling down the ramp?
The gravitational force can be represented by the vector F=0i-200j
In order to find the force we need to project vector F onto a unit vector in the direction of the ramp, so we use
v = cos(30°)i+(sin30°)j
After calculating the projection of F onto v, we get -100(cos(30°),(sin30°)). Taking the magnitude of this, we get that it takes a force of 100 pounds to keep the cart from rolling down the hill.
So I have a couple of questions about this.
First, why can we express force in pounds? Someone told me we can only express force in Newtons.
Second, I've seen others solve it this way:
The force required to keep the cart from rolling is 200×sin(30°)
And when they solve for the force perpendicular to the hill it is 200×cos(30°)
Why is it possible to calculate it this way as well?