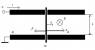
Let's look at a very crude model of an electric motor: the railgun. (scheme attached)
there are two conducting rails and a cylindrical conductive bar can roll on them freely. There is also a magnetic field perpendicular to the plane of the rails. The load is drawn by the rolling bar.
There are two governing equations for the motor: the Kirchoff loop equation and Newton's Second Law.
Let's start with Newton's Second Law for the bar. There are two forces acting on the bar:
Ampere's force: F_{a} = B l I
external force (opposite of what the force with which the bar pulls the load) - it is an external parameter F
The bar has mass m
The acceleration of the bar is a = dv/dt
So, Second Newton's Law gives:
<br />
m \, \frac{dv}{dt} = B L I - F<br />
Let's consider Kirchoff's Law now.
There are two voltage sources acting in the loop:
external voltage V which is an external force
induced EMF: E_{i} = -B L v
The resistance of the whole circuit is R.
The current through the circuit is I.
Second Kirchoff's Rule gives:
<br />
V - B L v = R I<br />
The mechanical variable for the system is v - the velocity of the bar (or, in rotary geometries the angular velocity of the rotor). The electric variable of the motor is the current passing through it I. The external parameters are the generated force F (or, generated torque in rotary geometries) and the applied voltage V. The internal parameters are the mass of the bar m (or, the moment of inertia of the rotor in rotary geometries), the length of the bar L, the magnetic field B and the total Ohmic resistance of all the conducting elements (rails and bar) R.
If you wish, you can eliminate the mechanical variable v completely and get an equation involving only the electric state variable I. Namely, solve the second equation with respect to v(t):
<br />
v(t) = \frac{V(t) - R I(t)}{B L}<br />
differentiate it with respect to time (keeping in mind that the external voltage as well as the current might vary in time)
<br />
\frac{dv}{dt} = \frac{V'(t) - R I'(t)}{B L}<br />
and substitute this into the first equation:
<br />
\frac{m}{B L} \left(V'(t) - R I'(t)\right) = B L I(t) - F(t)<br />
That is, we get a first order linear differential equation:
<br />
\frac{d I(t)}{d t} + \frac{(B L)^{2}}{m R} \, I(t) = \frac{1}{R} \left(V'(t) + \frac{B L}{m} F(t)\right)<br />
How is this equation like Ohm's Law? If anything, it looks like there is a capacitative element:
<br />
\begin{array}{l}<br />
v_{\mathrm{ef}} - \frac{Q}{C_{\mathrm{ef}}} = R_{\mathrm{ef}} \, I \\<br />
<br />
I = \frac{d Q}{d t}<br />
\end{array}<br />
<br />
\frac{d I}{d t} + \frac{1}{R_{\mathrm{ef}} C_{\mathrm{ef}}} I = \frac{V'_{\mathrm{ef}}(t)}{R_{\mathrm{ef}}}<br />
and, taking the effective resistance to be the same as the Ohmic resistance of the true motor (which can be done, by taking F = 0 - free running motor), then we see that the effective voltage applied on this circuit is:
<br />
V_{\mathrm{ef}} = V(t) + \frac{B L}{m} \int_{t_{0}}^{t}{F(t') \, dt'}<br />
i.e. it is time dependent even if the external parameters V(t) and F(t) are constant, and, the effective capacitance is:
<br />
C_{\mathrm{ef}} = \frac{m}{(B L)^{2}}<br />