- #1
Buzz Bloom
Gold Member
- 2,519
- 467
I searched for, but could not find any name or published value for a constant (with units m-3 K-3) which when multiplied by temperature (in degrees Kelvin) cubed gave the corresponding photon density (in m-3).
Does anyone know of such a constant with a published value?
I calculated a value, but it is very possible that this value may be incorrect. The value I calculated is:
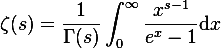
Regards,
Buzz
Does anyone know of such a constant with a published value?
I calculated a value, but it is very possible that this value may be incorrect. The value I calculated is:
20,286,839.73.
The expression I used is:8π (kB/hc)3 ∫0∞ x2 dx/(ex -1).
I calculated the integral numerically to get 2.4041137. I subsequently found out that the integral has the value:2 ζ(3),
where ζ is the Reimann zeta function.Regards,
Buzz