Question regarding the Biot-Savart Law and a Circular Loop

[TFM]

Homework Statement

The Biot-Savart Law states that the direction and magnitude of the magnetic field B
produced at a point P by a current length element I dl is given by:

$$d\vec{B} = \frac{\mu_0}{4\pi}\frac{Id\vec{l}\times \hat{r}}{r^2}$$

Where $$\hat{r} = \frac{\vec{r}}{r}$$

where r is the position vector from the current length element to the point P.

(i)

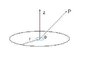
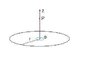
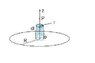
A circular loop of wire of radius R lies in the xy-plane and is centred at the origin.
The wire carries a steady current I, which is seen to be flowing clock-wise round the
loop when looking along the z-direction from the negative z towards the positive z.
Calculate the magnetic field at a distance Z on the axis of the circular loop and show
that the z-component of the field is given by:

$$B_z = \frac{\mu_oIR^2}{2(Z^2+R^2)^{3/2}}$$

(ii)

A single-turn, circular loop of radius 10 cm is to produce a field at its centre that
will just cancel the earth’s magnetic field at the equator, which is 0.7 G directed
north. Find the current in the loop (1 T ≡ 104 Gauss).

(iii)

Make a sketch, showing the orientation of the loop and the current for part (ii).

Homework Equations

Given in question

The Attempt at a Solution

Okay I'm doing part (i)

so far I have inserted R hat to give:

$$dB = \frac{\mu_0}{4\pi}\frac{Id\vec{l}\times\vec{r}}{r^3}$$

to get B I need to integrate:

$$B = \int \frac{\mu_0}{4\pi}\frac{Id\vec{l}\times\vec{r}}{r^3}$$

and I can take out a few items:

$$B = \frac{\mu_0}{4\pi} \int \frac{Id\vec{l}\times\vec{r}}{r^3}$$

But I am not sure where to go now.

Could anyone give me any suggestions?

?

TFM

 

[gabbagabbahey]

Find relevant expressions for $\vec{r}$, $r^3$ and $\vec{dl}$

 

[TFM]

Okay. Well, firstly:

$$d\vec{l}$$ is a line integral

$$r^3$$ is the distance from the point on the wire to where the Magnetic field is being measured

$$\vec{r}$$ is a vector, but I am not sure of what it represents...?

?

TFM

 

[gabbagabbahey]

Okay. Well, firstly:


$$\vec{r}$$ is a vector, but I am not sure of what it represents...?

?

TFM

You said it yourself in your first post:

$$\vec{r}$$ is the position vector from the current length element to the point P.

draw a picture, and try to express this in terms of cylyndrical coordinates and unit vectors...remember, since you are trying to find the field at "a distance Z on the axis of the circular loop", your point P is at $(r, \phi, z)=(0,0,Z)$

 

[TFM]

Is this the right diagram:

I think it should be the second one, since you stated:

draw a picture, and try to express this in terms of cylyndrical coordinates and unit vectors...remember, since you are trying to find the field at "a distance Z on the axis of the circular loop", your point P is at $$(r, \phi, z)=(0,0,Z)$$

?

TFM

 

[gabbagabbahey]

The second one is close, but you have mislabeled 'r'...the radius of the circular path of the wire is capital 'R', little 'r' should represent the distance form P to an infinitesimal length of the wire dl...you should shade in a short section of the wire and call it 'dl'...then find an expression for the vector from 'dl' to 'P'...

 

[TFM]

Okay so firstlty I have the midifed attached image (Its a JPEG, hence the reason the filling in is poor)

so I need an expression for the vector from dl to P. would it not be $$\hat{z}$$, since the point P is on the Z axis, and so the vector would go from the centre of the loop to P, which is just up along the Z-Axis

?

TFM

 

[gabbagabbahey]

P is on the z-axis, but dl is not!...So how could the vector $\hat{z}$ possibly go from dl to P?

 

[TFM]

I am slightly confused...Where is dl from?

TFM

 

[gabbagabbahey]

dl is an infinitesimal length of the wire...where is the wire? Pick a tiny section of the wire and call it dl...what are it's coordinates?

 

[TFM]

wire of radius R lies in the xy-plane and is centred at the origin.

I see now, the wire is a loop around the x-axis, not up down it. so a point on the z axis would be [tex] R^2 + Z^2 [\tex] from the wire?

TFM

 

[gabbagabbahey]

$$\sqrt{R^2+Z^2}$$ gives you the length of the vector $\vec{r}$, but you also need to know its direction...draw an arrow from dl to P...which way does it point?

 

[TFM]

Its pointing towards the Z-axis, but at an angle towards it, not parallel

?

TFM

 

[gabbagabbahey]

Okay, call that angle $\alpha$; then the direction of $\vec{r}$ is $-\cos \alpha \hat{r}+\sin \alpha \hat{z}$ Is it not?...now look at the triangle, what are $\cos \alpha$ and $\sin \alpha$ in terms of R and Z?

 

[TFM]

$$cos \alpha =\frac{Adjacent}{Hypotenuse}$$

$$sin \alpha =\frac{Opposite}{Hypotenuse}$$

Hypotenuse will be the lkine from I to P, and the adjacent will be R, opposite will be Z

TFM

 

[gabbagabbahey]

Yes, but isn't the length of the line from dl to P $\sqrt{Z^2+R^2}$?...what does that give you for $\vec{r}$?

 

[TFM]

Well:

$$cos\alpha = \frac{R}{\sqrt{Z^2 + R^2}}$$

and

$$sin\alpha = \frac{Z}{\sqrt{Z^2 + R^2}}$$

?

TFM

 

[gabbagabbahey]

Yes, and what does that make $\vec{r}$?

 

[TFM]

Well Since:

$$\hat{r} = -\cos \alpha \hat{r}+\sin \alpha \hat{z}$$

that would make:

$$\hat{r} = -\frac{R}{\sqrt{R^2 + Z^2}} \hat{r} + \frac{Z}{\sqrt{R^2 + Z^2}} \hat{z}$$

?

TFM

 

[gabbagabbahey]

Uggh...let's switch to $\hat{s}$ for the cylindrical unit vector so that yo don't confuse it with $\hat{r}$ which is the direction of the vector from dl to P...then you have:

$$\hat{r} = -\frac{R}{\sqrt{R^2 + Z^2}} \hat{s} + \frac{Z}{\sqrt{R^2 + Z^2}} \hat{z}$$

And since you've already found the magnitude of $\vec{r}$ to be $${\sqrt{R^2 + Z^2}$$...that means the vector $\vec{r}$ is...?

 

[TFM]

so:

$$\hat{r} = -\frac{R}{\sqrt{R^2 + Z^2}} \hat{s} + \frac{Z}{\sqrt{R^2 + Z^2}} \hat{z}$$

Would this make:

$$\vec{r} = {\sqrt{R^2 + Z^2}*(-\frac{R}{\sqrt{R^2 + Z^2}} \hat{s} + \frac{Z}{\sqrt{R^2 + Z^2}} \hat{z})$$

?

TFM

 

[gabbagabbahey]

Yes...now you need to find an expression for $$\vec{dl}$$

 

[TFM]

Wouldn't $$\vec{R}$$ be related to $$d\vec{l}$$? becasue isn't $$d\vec{l}$$ a little bit of $$\vec{R}$$?

TFM

 

[silur]

Check this:

http://planetphysics.org/encyclopedia/QuarterLoopExampleOfBiotSavartLaw.html