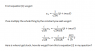Quick question about raising and lowering operators (ladder operators)

[PhysicsGirl90]

Reading through my QM text, I came across this short piece on ladder operators that is giving me trouble (see picture). What I am struggling with is how to get to equations 2 and 3 from equation 1.

Can someone point me in the right direction? Where does the i infront of the x go?

 

[tiny-tim]

Hi PhysicsGirl90!

Where does the i infront of the x go?

It disappeared when they multiplied the whole thing by the constant i/√(ωh)

 

[PhysicsGirl90]

Hey tiny-tim,

Thanks for your suggestion. I tried it but i get stuck trying to get the same equation as the text. I have included what i got so far in the picture. Can you give it a look and tell me what I am doing wrong?

 

[tiny-tim]

Hey PhysicsGirl90!

(just got up :zzz:)

the RHS of what you got is the same as in the text

(apart from a constant, and you can always multiply an eigenvector by any constant!)

 

[DrClaude]

This is a very sloppy "derivation" of the ladder operators. First of all

Simple algebraic factoring yields two roots

is not correct, since \hat{x} and \hat{p} are operators. (By the way, it should be d/dx, not d/d\hat{x}.) You can get inspiration from what algebraic factoring would give, if these were ordinary variables, in order to investigate operators that look like the roots. But a_+ and a_- are not "derived" this way.

You can also notice that \hat{X} = \sqrt{\frac{m \omega}{\hbar}} \hat{x} and \hat{P} = \frac{1}{\sqrt{m \hbar \omega}} \hat{p} are dimensionless.

 

[PhysicsGirl90]

Thanks again tiny-tim and thank you DrClaude for your help