Speedking96
- 104
- 0
Homework Statement
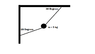
A 5 kg mass is attached to two ropes as indicated in the figure below. Find the tension in both ropes.
Homework Equations
Ʃy= 0 Ʃx = 0
The Attempt at a Solution
Mass of object: 5 * 9.81 = 49.05
T1 sin 30 - T2 cos 20 = 49.05
T1 cos 30 + T2 sin 20 = 0
Upon solving I get the T1 to be 17 Newtons and the T2 to be -43 Newtons.
It doesn't seem right to me.
Thank you.