Radius of Curvature Derivation for Bending of Beam w/Overhangs

[Freyster98]

Homework Statement

Derive an expression geometrically for the radius of curvature of the following beam. This is part of a lab assignment for the bending of a simply supported beam with overhangs.

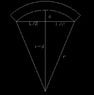
** I did this crappy diagram with AutoCAD, so I couldn't ( or didn't know how to ) include greek letters. Let's let r= $$\rho$$, and d= $$\delta$$ for my derivation.

Homework Equations

a²+b²=c²

The Attempt at a Solution

I just used the pythagorean theorem to solve for $$\rho$$.

Starting with: $$\rho$$²= ($$\rho$$-$$\delta$$)²+(L/2)².

Factoring out ($$\rho$$-$$\delta$$)² , solving for $$\rho$$ and simplifying , I end up with the following expression:

$$\rho$$=($$\delta$$/2)+(L²/8$$\delta$$)I guess I have this question...is this the proper way to derive the radius of curvature geometrically? Is it ok to do it this way?

 

[tiny-tim]

Derive an expression geometrically for the radius of curvature of the following beam.
…
I just used the pythagorean theorem to solve for $$\rho$$.

Starting with: $$\rho$$²= ($$\rho$$-$$\delta$$)²+(L/2)².

Factoring out ($$\rho$$-$$\delta$$)² , solving for $$\rho$$ and simplifying , I end up with the following expression:

$$\rho$$=($$\delta$$/2)+(L²/8$$\delta$$)

I guess I have this question...is this the proper way to derive the radius of curvature geometrically? Is it ok to do it this way?

Hi Freyster98!

(have a rho: ρ and a delta: δ )

Yes, Pythagoras is fine (though you seem to have lost a factor of 2 somewhere ).

But there is quicker method (with less likelihood of a mistake):

Hint: similar triangles ​

 

[Freyster98]

Hi Freyster98!

(have a rho: ρ and a delta: δ )

Yes, Pythagoras is fine (though you seem to have lost a factor of 2 somewhere ).

But there is quicker method (with less likelihood of a mistake):

Hint: similar triangles ​

I ran through it a few times...I don't see where I'm losing a factor of 2.

 

[tiny-tim]

sorry … my similar triangles method (have you tried that yet?) gave me the diameter, not the radius …

so i got an extra 2

 

[Freyster98]

sorry … my similar triangles method (have you tried that yet?) gave me the diameter, not the radius …

so i got an extra 2

Ok, thanks. No, I haven't tried the similar triangles because, well, I don't get it :uhh:

 

[tiny-tim]

Ok, thanks. No, I haven't tried the similar triangles because, well, I don't get it :uhh:

ok … the triangle with sides d and L/2 is similar to the triangle with sides L/2 and … ?