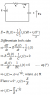RC circuit and Laplace transforms

[darkfeffy]

Hi everyone,

I know this should be obvious, but there's something I am just NOT getting.

Imagine a simple series RC circuit with a DC source as shown in the attachment. As can be seen from the picture, I have solved the differential equation in capacitor current in the time domain. In order to be able to solve the problem, I have assumed that dE/dt = 0 as this is a dc source.

I wish to know why I can't take the Laplace transform of both sides of the equation (*). I know that Laplace(0) = 0, so this would give a bogus equation (i.e. I(s) = 0, which is wrong). But if my equation (*) is right, then why can't I use the laplace transform of both sides at this point?

From textbooks, I read that the DC source is considered as a step input, thus in the Laplace domain, this would be E/s (in other words, the switch is closed at t=0). So, what is wrong with equation (*)?

Please don't hesitate to point out trivialities.

Thanks for your understanding.
e.

 

[Bob S]

\text{ Try }f(s) = \frac{1}{s-a} \space \text{ for } F(t) = 0 \text { for t <= 0 and } F(t)=e^{at} \text { for } t>0
There is no dc component for t>0. If you want a dc component, then try this online Laplace transform editor:

http://wims.unice.fr/wims/wims.cgi

Put in 1 - e^a*t and do Laplace to get
f(s) = \frac{1}{s}-\frac{1}{s-a}

 

[DragonPetter]

First, if you are just using laplace transforms, you should be able to solve this with a lot less steps. The sooner you go into the laplace domain, the easier it is. You rewrite x(t) as X(s). If it is going to be applied as a step function, multiply your source by (1/s). Any function f(t), i(t), v(t) etc. becomes F(s), I(s) and if it is integrated, divide the function by s, and if it is differentiated, multiply by s. When you study the laplace transform in diff eq. it is treated as an operator, something you can multiply, that takes place of the integragtion and differentiation.

The answer to your question though, is that you are integrating zero on the right hand side, and when you integrate 0, you get a constant. To solve for this constant, simply set your time variable to 0, and you will see that your constant is equal to the current, which is equal to V/R. This gives you your voltage as the switch is closed. Substitue V/R into this constant and solve for your current now, and you will see your answer.

 

[sophiecentaur]

Hi everyone,

In order to be able to solve the problem, I have assumed that dE/dt = 0 as this is a dc source.

If you assume dE/dt = 0 , doesn't that assume a steady state (i.e the situation long after the switch has been connected)?

 

[DragonPetter]

Also, I thought I should add, when you go to the step of setting your dE/dt to zero, you are basically changing your circuit. How is this? Well, if you start from the very beginning with your first equation, and take the laplace transform, assuming a step input, and then differentiate by multiplying both sides by s in the laplace domain, you end up E(s), rather than 0.

By changing to dE/dt to 0, you are only considering your steady state, and basically removing the step function of the switch.

This is why I recommended starting the laplace transform as soon as possible without nulling out important parts of the equation like your dE/dt.

 

[DragonPetter]

If you assume dE/dt = 0 , doesn't that assume a steady state (i.e the situation long after the switch has been connected)?

Yes, I think you're right that it is assuming steady state, and the differential equation * is setup as if the switch was already closed to begin with.