Reaction and friction coefficient on a cylinder

[Karol]

Homework Statement

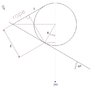
The cylinder weighs 200[N] and lies on a rough surface. a rope holds it in place.
What's the tension T in the rope and what's the minimal coefficient of friction.

Homework Equations

Friction: f=μN

The Attempt at a Solution

All the geometry i have drawn. T balances the torque made by the weight of the cylinder. i calculate torque round the point of contact with the inclined surface:
The distance d from the line of action of T:
$$d=\frac{R}{\tan30^0}\cdot \sin 60^0$$
Now the torque from the weight equals the torque from T:
$$200R\cdot \sin 30^0=T\cdot d\rightarrow T=66.7$$
It should be 654 and i don't continue yet to the friction coefficient.
Edit: i found my mistake, in Newtons it comes out right. now i will try to find the coefficient of friction

 

[mfb]

I get 654 N if the cylinder has a mass of 200 kg instead of a weight of 200N.

654/66.7=9.81 made the difference clear.