M_Abubakr
- 8
- 0
Homework Statement
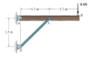
Consider beam “A-B” and strut “C-D” from Figure QA1. The beam “A-B” is hinged at point “A” and hinged with strut “C-D” at point “C”. It has an applied force of 8 kN applied at point B as shown in Figure QA1. Strut “C-D” is hinged at point “D” and it is also hinged with beam “A-B” at point “C”
Homework Equations
(a) Calculate the horizontal and vertical components of the reaction force at hinge “A”.
(b) Calculate the horizontal and vertical components of the reaction force on the beam at “C”.
The Attempt at a Solution
(a)
Summation of moments about point A.
-8x3+DCxCos(45)x1.5=0
DC=22.627kN
Summation of moments about C
1.5xAy-8x1.5=0
Ay=8kN
Summation of forces in x direction
Ax+DCSin45=0
Ax=-22.627Sin45
Ax=-16kN
(b)
DCx=22.627sin(45)
DCx=15.99kN = 16kN
DCy=22.627cos(45)
DCx=15.99kN=16kN
Is this correct?