EliasS
- 5
- 0
Homework Statement
Hello,
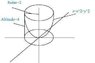
the problem ask you to pass this integral
\displaystyle\int_{-2}^{2}\int_{-\sqrt[ ]{4-x^2}}^{\sqrt[ ]{4-x^2}}\int_{x^2+y^2}^{4} x {dz}{dy}{dx}
to sphere coordinates, but I don't really know how
Homework Equations
Well, I know the basics formulas,
x=rho*sin(phi)*cos(theta)
y=rho*sin(phi)*sin(theta)
z=rho*cos(theta)
rho^2=x^2+y^2+z^2
tan theta=x/y
and all the average problems I know how to do them, but this one I can't see it
The Attempt at a Solution
The solution of the book is this, but I don't know how to get there, any clues?
\displaystyle\int_{0}^{2{\pi}}\int_{0}^{arctan(1/2)}\int_{0}^{4sec\phi} \rho^3 sin^2\phi cos\vartheta {d\rho}{d\phi}{d\vartheta}+\displaystyle\int_{0}^{2{\pi}}\int_{arctan(1/2)}^{\pi/2}\int_{0}^{cot\phi csc\phi} \rho^3sin^2\phi cos\phi{d\rho}{d\phi}{d\vartheta}
Thank you