Proving X, A, and Y Lie in a Straight Line | Triangle Medians Proof

  • Thread starter Thread starter Jarvis Bull Dawg
  • Start date Start date
AI Thread Summary
To prove that points X, A, and Y lie in a straight line, the discussion emphasizes using indirect proof and constructing specific segments. By connecting points C and X, as well as B and Y, a clearer geometric figure emerges that aids in the proof. The importance of a precise drawing is highlighted to visualize the relationships between the points. The conversation suggests that careful analysis of the triangle's medians and their extensions will lead to the desired conclusion. A thorough understanding of triangle properties is essential for this proof.
Jarvis Bull Dawg
Messages
17
Reaction score
0
This is question I am really stuck with, please help if you can. (Its by indirect proof).
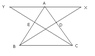
Question: The medians BD and CE in triangle ABC are produced to X and Y respectively so that BD = DX and CE = EY. Prove that X, A, and Y lie in a straight line.
 
Last edited:
Physics news on Phys.org
Here is what I have so far:
 

Attachments

  • Diagram1.GIF
    Diagram1.GIF
    1 KB · Views: 552
Last edited:
No need in absurdum!

Connect C and X and see what helpful figure you are getting.
Same for B and Y.
Precise drawing would help.
 

Thread 'Finding the number of ways to arrange identical balls in a circle (3 different colors)'

I tried to combine those 2 formulas but it didn't work. I tried using another case where there are 2 red balls and 2 blue balls only so when combining the formula I got ##\frac{(4-1)!}{2!2!}=\frac{3}{2}## which does not make sense. Is there any formula to calculate cyclic permutation of identical objects or I have to do it by listing all the possibilities? Thanks
View full post »

Thread 'Making the denominator of a certain fraction real'

Essentially I just have this problem that I'm stuck on, on a sheet about complex numbers: Show that, for ##|r|<1,## $$1+r\cos(x)+r^2\cos(2x)+r^3\cos(3x)...=\frac{1-r\cos(x)}{1-2r\cos(x)+r^2}$$ My first thought was to express it as a geometric series, where the real part of the sum of the series would be the series you see above: $$1+re^{ix}+r^2e^{2ix}+r^3e^{3ix}...$$ The sum of this series is just: $$\frac{(re^{ix})^n-1}{re^{ix} - 1}$$ I'm having some trouble trying to figure out what to...
View full post »

Similar threads

Is (y + z)x1 = (y1 + z1)x the equation of a straight line in 3D space?
Replies
17
Views
2K
(Rigorously) Prove that two medians of a triangle intersect
Replies
2
Views
3K
Prove Homothetic Triangles Concurrent: Ceva's Theorem
Replies
1
Views
2K
Triangle with median and altitude
Replies
2
Views
2K
Find Length of Median in Triangle via Cosine Law
Replies
2
Views
2K
Prove the sums of the angles of any given triangle = 180°
Replies
12
Views
3K
Reflection of triangle over a line
Replies
15
Views
4K
Intersection of a circle and a sine curve
Replies
26
Views
684
Find the third coordinate of a vertex of an equilateral triangle
Replies
11
Views
10K
MHB Geom Ch: Prove $AB=x^3$ Given $\triangle ABC$ & $\triangle AEF$
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top