You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How is the Refracting Angle of a Prism Calculated Using θ and θ/2?
AI Thread Summary
The discussion focuses on calculating the refracting angle of a prism using the angles θ and θ/2, highlighting that this is primarily a geometric problem rather than a purely optical one. The incident light makes an angle of A/2 to the surface, and reflections at this angle lead to a divergence of 2A, which corresponds to θ. The conversation also touches on the concept of total internal reflection and the conditions under which it occurs, emphasizing that the surrounding medium influences this phenomenon. Additionally, the participants clarify the geometric properties of cyclic quadrilaterals and how they relate to the angles involved in the prism's configuration. Overall, the thread provides insights into the mathematical relationships governing light behavior in prisms.
Physics news on Phys.org
Outrageous
- 373
- 0
One more question , why the light ray from the collimator reflected not refracted?
Thank you.
Thank you.
rude man
Science Advisor
- 8,032
- 869
Is the prism immersed in a spherical liquid of n > n of prism? Then you can get total internal reflection of the incoming beam back into the sphere.
Outrageous
- 373
- 0
No, the outside medium is air. I read and checked books but I can't find one to prove θ/2=refracting angle of prism. Please guide . Thank you.
- 42,656
- 10,435
Not sure I understand the picture. It looks like a circular prism with a triangular hollow.
rude man
Science Advisor
- 8,032
- 869
haruspex said:Not sure I understand the picture. It looks like a circular prism with a triangular hollow.
Which could account for total internal reflection back into the circular prism.
Outrageous
- 373
- 0
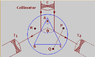
ABC is a transparent prism .
A is the refracting angle of a prism.
T is telescope to receive the reflected light.
This is an experiment to find A.
A lot of books did say this is an easy way to find A . But I can't find how . Please guide. Thank you.
A is the refracting angle of a prism.
T is telescope to receive the reflected light.
This is an experiment to find A.
A lot of books did say this is an easy way to find A . But I can't find how . Please guide. Thank you.
- 42,656
- 10,435
Ok, so this nothing to do with refraction. It's simply a geometry problem. The prism might as well be a pair of mirrors at angle A.
The incident light makes an angle A/2 to the surface, and is reflected at angle A/2 to the surface. Therefore each reflection is at angle A to its corresponding incident ray. Since the rays each side are turned through angle A in opposite directions, they now diverge at angle 2A = theta.
The incident light makes an angle A/2 to the surface, and is reflected at angle A/2 to the surface. Therefore each reflection is at angle A to its corresponding incident ray. Since the rays each side are turned through angle A in opposite directions, they now diverge at angle 2A = theta.
Outrageous
- 373
- 0
How do we make the incident light at an angle A/2 to the surface of mirror?haruspex said:The incident light makes an angle A/2 to the surface, and is reflected at angle A/2 to the surface.
How to know reflection is at angle A to its incident ray ? or do you mean the incident light makes an angle A/2 to the normal?haruspex said:Therefore each reflection is at angle A to its corresponding incident ray. Since the rays each side are turned through angle A in opposite directions, they now diverge at angle 2A = theta.
Thank you
- 42,656
- 10,435
Simple geometry. Draw a line bisecting the angle A. It is parallel to the incident beam, so that line and the beam make the same angle to the surface.Outrageous said:How do we make the incident light at an angle A/2 to the surface of mirror?
However, it is important that it does not need to be exactly A/2. Suppose you set it up a little bit askew, so the beam makes an angle A/2+x to one surface, and therefore an angle A/2-x to the other.
A reflected beam makes the same angle to the surface as the incident beam, so these are also A/2+x, A/2-x respectively. One beam is therefore 'turned' through an angle of A+2x, the other through an angle of A-2x,. Adding these up still gives 2A as the divergence between them.
Outrageous
- 373
- 0
Totally understand already . Really thank you . No wonder physics books don't show, it is just a math problem. Thank you so much
Outrageous
- 373
- 0
http://www.pinkmonkey.com/studyguides/subjects/physics/chap16/p1616601.asp
Can you please explain to me why AQRS is a cyclic quadrilateral?
Thank you
Can you please explain to me why AQRS is a cyclic quadrilateral?
Thank you
- 42,656
- 10,435
It doesn't define the point R, but it looks like it is chosen as the point where the normals at Q and S intersect. So by definition the angles that AR subtends at Q and S are each right angles. That makes AQRS a cyclic quadrilateral, i.e. its vertices lie on a circle, and AR is a diameter of that circle.Outrageous said:http://www.pinkmonkey.com/studyguides/subjects/physics/chap16/p1616601.asp
Can you please explain to me why AQRS is a cyclic quadrilateral?
Outrageous
- 373
- 0
But do we have enough to prove Q and S are lie on the circumference?
Use the centre of circle?
Use the centre of circle?
- 42,656
- 10,435
Yes. You can define a circle uniquely by declaring that AR is diameter. Any right-angled triangle you then draw with AR as hypotenuse will have its third vertex on the circumference of the circle. This is pretty basic geometry.Outrageous said:But do we have enough to prove Q and S are lie on the circumference?
Use the centre of circle?
Outrageous
- 373
- 0
Yup, you are totally correct.
Thank you.
Thank you.
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 3
- Views
- 4K
- Replies
- 9
- Views
- 5K
- Replies
- 26
- Views
- 3K
- Replies
- 3
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 7
- Views
- 6K
- Replies
- 4
- Views
- 3K
- Replies
- 15
- Views
- 2K
- Replies
- 11
- Views
- 2K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 25
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math