Related: Center of Mass, Torque, and Tension on a String. Find θ, m1, and m2.

[DavidAp]

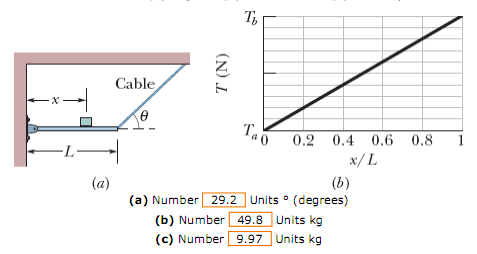
Figure 12-52a shows a horizontal uniform beam of mass mb and length L that is supported on the left by a hinge attached to a wall and on the right by a cable at angle θ with the horizontal. A package of mass mp is positioned on the beam at a distance x from the left end. The total mass is mb + mp = 59.8 kg. Figure 12-52b gives the tension T in the cable as a function of the package's position given as a fraction x/L of the beam length. The scale of the T axis is set by Ta 500 N and Tb 700 N. Evaluate (a) angle θ, (b) mass mb, and (c) mass mp.

The answers are displayed at the bottom of the diagrams.

Related Equation:
T = r*Fτ

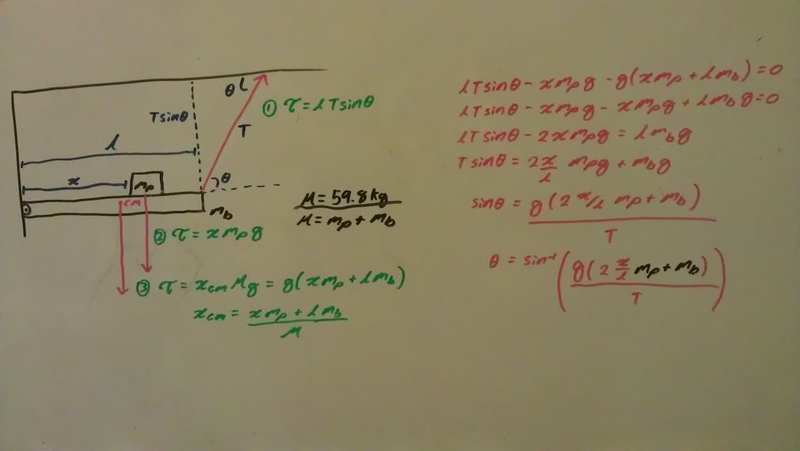
My attempt at this problem can be seen in the image below. I decided to write it on my board to make it easier to follow and less strenuous on the eyes; however, if my handwriting is illegible please do not hesitate to tell me for I will retype it for you as a response. Although my work below doesn't show it I have been tackling this problem for over an hour on various sheets of paper and have been able to get no where so any help is much appreciated.

I feel as if I am suppose to isolate mp+mb so that I may replace it with M but in my final equation I am unable to due so because 2x/l is being multiplied to mp. As for x/l and T, if I am able to isolate mp+mb, I was just planning on picking a random point on the chart above to place into my equation. Is this what I'm suppose to do?

Thank You for taking the time to review my question.

(note) I'm sorry if the size of my image creates any inconveniences.
(edit) Small grammar mistakes.

 

[BruceW]

You've got the right idea by calculating the total torque around the hinge and equating it to zero. But You haven't calculated it right.

l \ T \ sin(\theta)=g(m_p+m_b)x_{cm}
This is what you should be trying to get, so you need to calculate the value of x_{cm} correctly.

So first, you need to think what is the centre of mass of the beam, and use that to find the centre of mass of the two objects combined.

I'm guessing you already know it, but just in case, this is the equation for the centre of mass of a collection of masses:
x_{cm} = \frac{\Sigma m_i \ x_i}{\Sigma m_i} = \frac{\int \ \mu_{(x)} x \ dx}{\int \ \mu_{(x)} \ dx}

Which is the representation in the non-continuous and continuous cases. (\mu is the linear density - ie mass per length).

 

[DavidAp]

You've got the right idea by calculating the total torque around the hinge and equating it to zero. But You haven't calculated it right.

l \ T \ sin(\theta)=g(m_p+m_b)x_{cm}
This is what you should be trying to get, so you need to calculate the value of x_{cm} correctly.

So first, you need to think what is the centre of mass of the beam, and use that to find the centre of mass of the two objects combined.

I'm guessing you already know it, but just in case, this is the equation for the centre of mass of a collection of masses:
x_{cm} = \frac{\Sigma m_i \ x_i}{\Sigma m_i} = \frac{\int \ \mu_{(x)} x \ dx}{\int \ \mu_{(x)} \ dx}

Which is the representation in the non-continuous and continuous cases. (\mu is the linear density - ie mass per length).

So the centre of mass of the beam, disregarding the package on top, should be the center of the beam. I did some quick integration and it was right.
Xcm = ∫(0,l) xρdx / ∫(0,l) ρdx = ρ(X^2 / 2)(0, l) / ρ(X)(0,l) = (l^2 / 2)/(l) = l/2

Once I have that do I use a series to calculate the center of mass of the two body system?
Xcm = (l/2 mb + xmp)/M?

If so I'm not quite sure how this helps assuming that my two previous equations for torque where right.
1) Torque = lTsinθ
2) Torque = xgmp >>> I'm starting to think that I shouldn't have this but this is a force in the system to I'm hesitant to remove it. However, even if I did remove it...
3) Torque = g(l/2 mb + xmp) >>> I'm not sure how this would help.

What should I do?

 

[BruceW]

So the centre of mass of the beam, disregarding the package on top, should be the center of the beam. I did some quick integration and it was right.
Xcm = ∫(0,l) xρdx / ∫(0,l) ρdx = ρ(X^2 / 2)(0, l) / ρ(X)(0,l) = (l^2 / 2)/(l) = l/2

Once I have that do I use a series to calculate the center of mass of the two body system?
Xcm = (l/2 mb + xmp)/M?

This is exactly right.

2) Torque = xgmp >>> I'm starting to think that I shouldn't have this but this is a force in the system to I'm hesitant to remove it. However, even if I did remove it...

Yes, you need to remove this, because it is already accounted for when you combined the two bodies to get their centre of mass.

1) Torque = lTsinθ ... 3) Torque = g(l/2 mb + xmp)

Now you equate these two torques (since they must cancel). And if you imagine T as y and x/L as x, you've got a straight line of y against x. The graph gives you this, so you get two pieces of information - the intercept and the gradient. You need to use both of these to find the answer.