How can the water level in a trough be calculated using related rates?

iRaid
Messages
558
Reaction score
8

Homework Statement


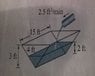
12.) A trough is 15ft long and 4ft across the top as shown in the figure. Its ends are isosceles triangles with height 3ft. Water runs into the trough at the rate of 2.5 ft3/min. How fast is the water level rising when it is 2 ft deep?

Homework Equations


The Attempt at a Solution



Not sure how to do this..
dv/dt = 2.5

I tried using the volume of a triangular prism: V=(1/2)bhl but no success.. I think the problem is IDK which numbers to use for the volume equation?
Can someone point me in the correct direction?
 

Attachments

  • d.jpg
    d.jpg
    6.9 KB · Views: 488
Last edited:
Physics news on Phys.org
Edit: Attached picture
 
If anyone is looking at this, what you have to do is find the area of the water, not the actual triangular prism.
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

How Fast Is the Water Level Rising in a Trough as It Fills?
Replies
1
Views
3K
Related rates (prism with a trapezoid base)
Replies
3
Views
2K
Rate of change of a triangular prisim
Replies
2
Views
1K
Calculating Minimum Water Level in a Barrel using ODE: Analysis and Approach
Replies
3
Views
1K
Isosceles Triangle related rates problem
Replies
5
Views
9K
Finding the Rate of Change of Water Height in a Filling Cylindrical Tank
Replies
11
Views
2K
Isosceles Triangular Prism Related Rates Problem
Replies
8
Views
13K
How to Calculate Water Level Changes in a Filling Trough
Replies
4
Views
2K
Related Rates: Water Trough Volume and Rate of Change
Replies
7
Views
5K
Finding Rate of Change for Water Level in a Trough
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top