MaHo12345
- 3
- 0
- TL;DR Summary
- I am trying to identify the relationship between pressure and flow in a proportional valve, considering the flow conditions.
Hi,
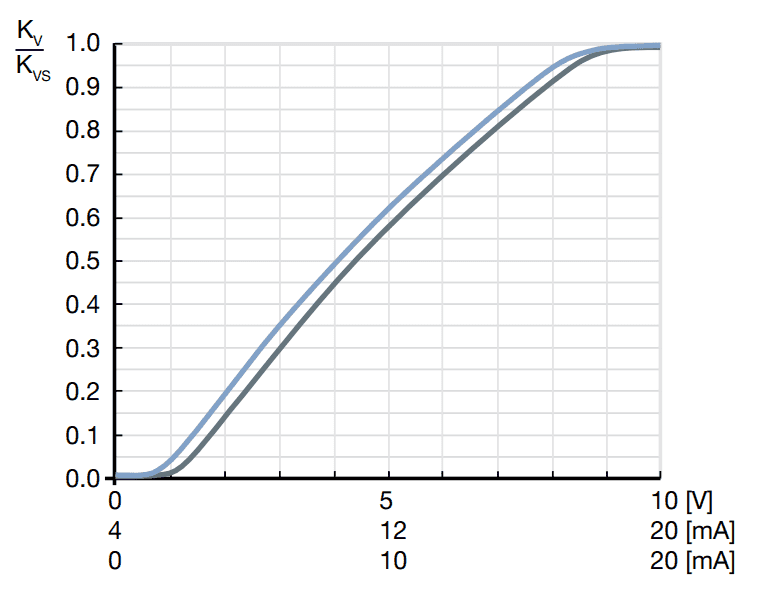
I have a valve which is connected to a pipe on both sides. I measure the pressure upstream of the valve. Downstream of the valve is a screw pump. I control my valve using an analog voltage input between 0 and 10 volts. According to the datasheet, the relationship between the analog input and ##\frac{K_v}{K_{vs}}## is as follows.
I also plotted the relationship between the voltage and the pressure upstream of the valve and got the following curve
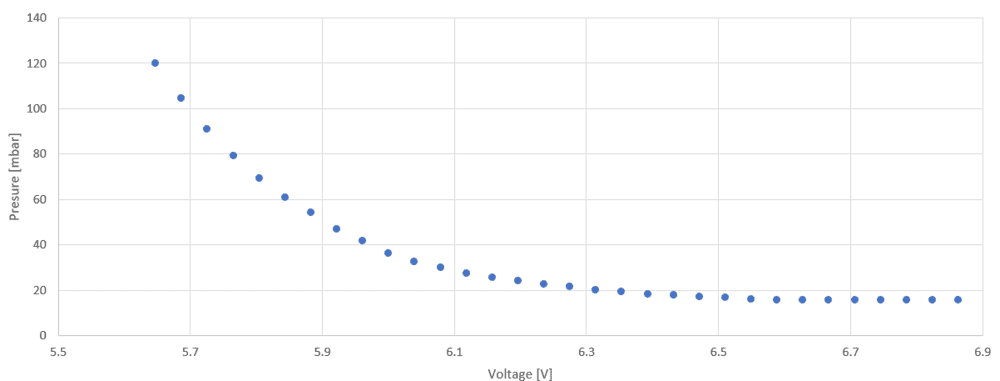
As visible, the pressure does not increase the same way as ##\frac{K_v}{K_{vs}}##. My questions to this are as follows:
1. What is actually plotted in the first plot? Does this ##\frac{K_v}{K_{vs}}## correspond to orifice size? In this case, I am correct to say that the flow rate increases linearly with the voltage applied to the valve?
2. Why do I get the pressure-voltage relationship as show in the second curve? What would be the mathematical relationship describing this behaviour?
I have already had a few thoughts, however I could not recreate the behaviour of the second graph. I think I must calculate the ##K_{vs}## value for each specific pressure drop. However, I only know the pressure drop (as I measure it) but I do not know the flow rate. Can anybody point me in the right direction?
I have a valve which is connected to a pipe on both sides. I measure the pressure upstream of the valve. Downstream of the valve is a screw pump. I control my valve using an analog voltage input between 0 and 10 volts. According to the datasheet, the relationship between the analog input and ##\frac{K_v}{K_{vs}}## is as follows.
I also plotted the relationship between the voltage and the pressure upstream of the valve and got the following curve
As visible, the pressure does not increase the same way as ##\frac{K_v}{K_{vs}}##. My questions to this are as follows:
1. What is actually plotted in the first plot? Does this ##\frac{K_v}{K_{vs}}## correspond to orifice size? In this case, I am correct to say that the flow rate increases linearly with the voltage applied to the valve?
2. Why do I get the pressure-voltage relationship as show in the second curve? What would be the mathematical relationship describing this behaviour?
I have already had a few thoughts, however I could not recreate the behaviour of the second graph. I think I must calculate the ##K_{vs}## value for each specific pressure drop. However, I only know the pressure drop (as I measure it) but I do not know the flow rate. Can anybody point me in the right direction?
Last edited: