I Relationship between the radius and area of liquid in a cylinder

[JohnnyGui]

Hello,

I did a calculation to determine whether a liquid with a fixed volume $V$, would be spread over a larger surface area $A$ on the inside mantle of a cylinder, if the cylinder has a larger radius $r$. So I’d like to find a relationship between the radius $r$ and the area $A$ over which the liquid is spread in the cylinder. The length of the cylinder $L$ and the volume of liequid $V$ are fixed.

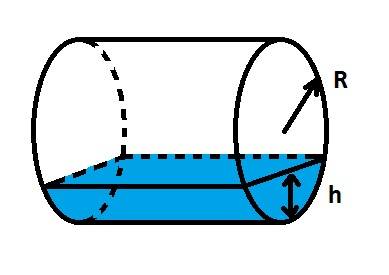
If the liquid with volume $V$ is put in the cylinder with a radius $r$, it would have the following picture when cut through;

- The area $O$ is formulated as: $\frac{r^2}{2} \cdot (θ – sin(θ)) = O$.
- The volume $V$ of the liquid would therefore be defined as: $\frac{r^2}{2} \cdot (θ – sin(θ)) \cdot L =V$.
- The area $A$ of the inside “mantle” of the cylinder over which the liquid is spread is defined as $L \cdot r \cdot θ = A$.

Combining these formulas will give the relationship of V, θ, r and A in the following form:
$$\frac{2V}{r(1-\frac{sin(θ)}{θ})} = A$$
The radius $r$ can be formulated in terms of θ as well since $\sqrt{\frac{2V}{L(θ-sin(θ))}}=r$. The end formula being:
$$\frac{2V}{\sqrt{\frac{2V}{L(θ-sin(θ)}} \cdot (1-\frac{sin(θ)}{θ})} = A$$
Plotting the relationship $\sqrt{\frac{2V}{L(θ-sin(θ))}}=r$ with θ being the variable, $V$ and $L$ being fixed values, shows a peculiar graph:

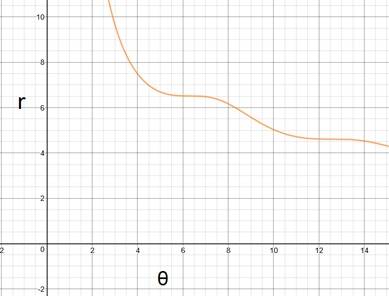
There are points in the graph of which the slope is actually zero, which means that a change in θ doesn’t give a change in radius. Looking at the graph as if the radius is the variable (which is my initial question) thus says that there are values of $r$ in which the change θ is vertical, as if it means that the radius $r$ doesn’t need to change to make θ change. I’m not sure how to interpret this.
How is this possible if the length $L$ and the volume of the liquid $V$ are fixed?

 

[mfb]

$\theta$ is only meaningful up to 2 pi, the first point where the derivative goes to zero. Your cylinder is nearly filled close to this value, increasing the radius a tiny bit leads to a large change in the angle, with a diverging ratio where the cylinder is exactly full.

There is an angle that minimized the area for a given volume. Here is a plot.

 

[JohnnyGui]

$\theta$ is only meaningful up to 2 pi, the first point where the derivative goes to zero. Your cylinder is nearly filled close to this value, increasing the radius a tiny bit leads to a large change in the angle, with a diverging ratio where the cylinder is exactly full.

There is an angle that minimized the area for a given volume. Here is a plot.

Ah, can't believe I missed this. Furthermore, shouldn't $\theta$ only be meaningful up to $\pi$ instead of $2\pi$ since an angle higer than $\pi$ would give negative values? So with the mentioned formula I can only calculate the area up until the liquid is filling half of the circle?

 

[mfb]

Negative values of what? The sine gets negative, but $\theta - \sin \theta$ stays positive. All your formulas work up to 2 pi. 2 pi corresponds to a fully filled cylinder.

 

[JohnnyGui]

Negative values of what? The sine gets negative, but $\theta - \sin \theta$ stays positive. All your formulas work up to 2 pi. 2 pi corresponds to a fully filled cylinder.

Just checked, and it does indeed work. The truth is that for the picture:

I derived a formula myself first, for the area $O$, which is:
$$r^2 (\frac{\theta}{2} - sin(\frac{\theta}{2}) \cdot cos(\frac{\theta}{2}))$$
I thought that if $\theta ≥ \pi$, this formula would give an erroneous area of $O$ since I'm deriving the side lengths of triangles with an angle $\theta$, and thus an angle can not exceed $\pi$.

However, it does give correct answers even if $\theta ≥ \pi$ and plots the exact same graph as $\frac{r^2}{2}(\theta - sin(\theta))$.
But I can't really deduce how:
$$r^2 (\frac{\theta}{2} - sin(\frac{\theta}{2}) \cdot cos(\frac{\theta}{2})) = \frac{r^2}{2}(\theta - sin(\theta))$$
Which means that:
$$cos(\frac{\theta}{2}) \cdot sin(\frac{\theta}{2}) = \frac{1}{2} \cdot sin(\theta))$$
Is there a way to prove this equation?

 

[SlowThinker]

$$cos(\frac{\theta}{2}) \cdot sin(\frac{\theta}{2}) = \frac{1}{2} \cdot sin(\theta))$$
Is there a way to prove this equation?

http://www.themathpage.com/atrig/double-proof.htm links to sum formulas, which links to a nice proof.

 

[JohnnyGui]

http://www.themathpage.com/atrig/double-proof.htm links to sum formulas, which links to a nice proof.

Thanks for the link. So I was still a bit surprised about how the formula still works if $\theta > \pi$ and I've drawn this scenario where the liquid has fillled more than half the circle:

At first glance, to calculate the circle area $O$ of the liquid I'd say that:
$$r^2 \cdot (cos(\frac{2\pi - \theta}{2}) \cdot sin(\frac{2\pi - \theta}{2}) + \frac{\theta}{2}) = O$$
This formula seems to give the same plot as the initial formula for $O$ that I've posted in my opening post, so that

$$r^2 \cdot (cos(\frac{2\pi - \theta}{2}) \cdot sin(\frac{2\pi - \theta}{2}) + \frac{\theta}{2}) = r^2 (\frac{\theta}{2} - sin(\frac{\theta}{2}) \cdot cos(\frac{\theta}{2}))$$
Thus, the initial formula still gives valid answers for $\theta > \pi$ up until $2\pi$

Bet there's also a way to prove this equation?