Relationships between Current, Voltage and Resistance

[fictionistruth]

Homework Statement

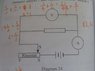
Based on the diagram attached, how do the values of current, I and voltage, V change when the sliding contact S of the rheostat is slowly moved from X to Y?

Homework Equations

Ohm's Law
R=V/I

The Attempt at a Solution

I used Ohm's Law to solve this question. My answer was: I decreases and V increases, because R is directly proportional to V and inversely proportional to I. As S is moved from X to Y, the resistance increases. I deduced that the voltage increases as resistance increases, and current decreases as resistance increases.

However my answer was wrong; the correct answer was: I decreases and V decreases. I don't understand why the voltage would decrease as resistance was increased because Ohm's Law clearly shows that R is directly proportional to V. Can anyone please explain why?

 

[mfb]

V and inversely proportional to I.

That is not true. You can re-write Ohm's law as RI=V. As you can see, V and I are proportional to each other. Another way to read R=V/I is "V and I have a constant ratio" (which is the same as "are proportional to each other").

As S is moved from X to Y, the resistance increases.

The total resistance increases, indeed.