Relative Velocity-Boat Problem and Minimization

[gbean]

Homework Statement

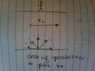
Fred's friends are in a boat. If they could travel perpendicularly to the shore, they could land at his position. However, a strong current vc is greater than the maximum vm of the motor. Find the magnitude of the angle, measured relative to the straight-across direction, at which his friends should point the boat to minimize the distance Fred has to walk.

a) arcsin (vm/vc)
b) arctan (vc/vm)
c) tan (vc/vm)
d) arctan (sqrt(vc/vm))

Homework Equations

a^2 + b^2 = c^2
sin(theta) = opposite/hypotenuse (=> theta = arcsin(opposite/hypotenuse))
cos(theta) = adjacent/hypotenuse
tan(theta) = opposite/adjacent
vx = vcos(theta)
vy = vsin(theta)
v = vx+vy

The Attempt at a Solution

I tried to draw this out and I get that the angle is represented by theta = arctan(vm/vc).

I don't know what I'm doing wrong, please help!

 

[gbean]

I know that the answer is A, but I still keep getting arcctan...

 

[diazona]

It's not clear from the diagram that you understand what \vec{v}_c and \vec{v}_m are. \vec{v}_c is the velocity of the current (relative to the shore), and \vec{v}_m is the velocity of the boat (hint: relative to what?).

 

[gbean]

Relative to an observer on the shore, aka Fred?

 

[gbean]

Vm is the velocity perpendicular to the shore, and then Vc is the velocity parallel to the shore?

 

[diazona]

Relative to an observer on the shore, aka Fred?

Nope. Think about this: v_m represents the speed at which the motor is able to push the boat. What is the motor pushing against? Therefore, what should the velocity \vec{v}_m be measured against?

 

[gbean]

The motor is pushing against vc, the current?

 

[diazona]

Well... sure, you could say that. So what is \vec{v}_m relative to?

 

[gbean]

To the current? I'm not totally sure what I'm supposed to be gleaning.

 

[diazona]

To the current?

Yep.

I'm not totally sure what I'm supposed to be gleaning.

So how could you express the velocity of the boat relative to the shore?

 

[gbean]

Vo = Vm + Vc

Vo = velocity relative to the shore
Vm = velocity of boat
Vc = velocity of current

 

[diazona]

OK, good. (I took a few minutes to work through it to make sure I wasn't leading you down the wrong track)

Now, the velocity of the current \vec{v}_c is fixed, but the velocity of the boat relative to the current, \vec{v}_m, can be pointed in any direction. So I would suggest drawing a new diagram of the river. Include the vector \vec{v}_c and a circle representing all the possibilities for \vec{v}_m.

 

[gbean]

Like this?

 

[diazona]

Kind of like that, but put the tail of \vec{v}_m (the center of the circle) at the tip of \vec{v}_c, because you're adding them.

 

[gbean]

So like this?

 

[diazona]

Sure, I guess that'll work. Now which orientation of \vec{v}_m satisfies the conditions of the problem?

 

[gbean]

Vm pointing to the left, or upstream.

 

[diazona]

No; if \vec{v}_m points directly upstream, parallel to \vec{v}_c, the boat will never reach the shore. Do you understand why?

Here's the way to think about it: when you add two vectors using the tail-to-tip method, the sum is a vector pointing from the tail of the first one (\vec{v}_c) to the tip of the second one (\vec{v}_m). The tip of the second vector, in this case, is on the circumference of the circle. So the sum \vec{v}_0 (that's what you called it, right?) should be drawn from the tail of \vec{v}_c to a point on the circle. Of all the possible vectors you can draw this way, which one gets the boat to the shore closest to Fred?

 

[gbean]

This is what I intuitively want vm to point, but I can't explain it...

 

[NewtonianAlch]

Hmm, you said you know the answer is A right? Have you considered drawing that situation to fit that model and seeing why it is so?

Vm should be the vector going towards Fred on the other side but at an angle, and Vc should be the vector going parallel to him, i.e. upstream/downstream.

Therefore to satisfy the triangle, one more side needs to be drawn, and that is the resultant vector that hopefully gets the boat straight to him.

 

[diazona]

This is what I intuitively want vm to point, but I can't explain it...

Yes, that is exactly the right configuration of vectors. Now you have a triangle; what can you conclude about any of the angles of that triangle?

 

[gbean]

45-45-90, but why?

 

[diazona]

45-45-90, but why?

How would I know? You're the one who came up with those numbers

Seriously though, that's not correct. Here's a hint: you can only know the numeric value of one of the angles in the triangle. Which one, and what is it? (And how do you know?)