Relatively simple vectors question, but no numbers....

In summary, the conversation is about finding the net force on point C due to two equal and opposite forces acting on it from points A and B. The equation used is the superposition of force principle, and the solution involves breaking the forces into components and using a 1-1-sqrt(2) triangle to simplify the calculation. The answer is found to be (2/sqrt(2)) * FAonC or sqrt(2) * FAonC. The conversation also mentions that the charges on points A and B are assumed to be of the same polarity.
  • #1
Bagwan
6
0
The unit right now is electrostatics, but this question is really just vectors, nothing to do with charges or anything... anyways here is the info:

1. Homework Statement
Three identical point charges, A, B, and C are located as shown here:

M9bYJ9L.png


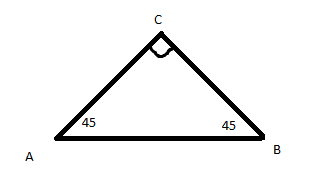
The force A-on-C is the same as the force B-on-C. What is the net force on C?

Homework Equations



I think the only equation I need is the superposition of force principle:
FnetC = FAonC + FBonC

The Attempt at a Solution


[/B]
Breaking into components (not allowed to use cosine law for some reason):

I know X-axis force is 0 as the 2 forces cancel out (since they are both equal and in opposite directions).

FnetCY = FAonC * cos(45) + FBonC * cos(45)

Not sure what else I can do though...

EDIT: I messed around with the 1-1-sqrt(2) triangle and I'm not sure if this is right, but is (2/sqrt(2)) * FAonC the right answer?

EDIT 2: Yes, that's the right answer, but sqrt(2) * FAonC is also right.

Because guess what, 2 divided by squareroot(2) is THE SAME THING AS squareroot(2)...
 
Last edited:
Physics news on Phys.org
  • #2
seems okay to me
 
  • #3
assuming the charges on the charges on the corners A and B are all the same polarity
 
  • #4
rpthomps said:
assuming the charges on the charges on the corners A and B are all the same polarity

Yeah they are all identical.

rpthomps said:
seems okay to me

How would I use the 1-1-squareroot2 triangle to simplify it more? I'm not sure how to do that part too well.
 
  • #5
replace your cos45 statement with the equivalent ratio
 

FAQ: Relatively simple vectors question, but no numbers....

What are vectors?

Vectors are mathematical quantities that have both magnitude and direction. They are commonly used in physics and engineering to represent forces, velocities, and other physical quantities.

What are the components of a vector?

A vector has two components: magnitude and direction. The magnitude is the length of the vector, while the direction is the angle at which the vector is pointing.

How are vectors represented?

Vectors are usually represented as arrows, with the length of the arrow representing the magnitude and the direction of the arrow representing the direction of the vector. They can also be represented using coordinates in a coordinate system.

What is the difference between a scalar and a vector?

A scalar is a quantity that has only magnitude, while a vector has both magnitude and direction. Examples of scalars include temperature, mass, and time, while examples of vectors include displacement, velocity, and force.

How do you add vectors?

To add vectors, you can use the parallelogram law or the head-to-tail method. With the parallelogram law, you draw the two vectors as adjacent sides of a parallelogram and the resultant vector is the diagonal of the parallelogram. With the head-to-tail method, you draw the tail of the second vector at the head of the first vector and the resultant vector is the vector from the tail of the first vector to the head of the second vector.

Similar threads

Vectors Directions: Where is this Resultant Vector Pointing?
Replies
14
Views
829
How to understand typo in MIT OCW chapter on Poynting vector?
Replies
4
Views
396
Displacement problem with unit vectors
Replies
4
Views
1K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
492
Elliptical motion in polar coordinates
Replies
10
Views
805
Find the value of ##\theta## when the Vx and Vy components are the same
Replies
12
Views
2K
A moving boat with a flag on its mast
Replies
15
Views
535
Syntax Error? x and y components of E field in unit vector form
Replies
13
Views
1K
Solving 2-D vector along three directions (say at 0,60 and 120 degree)
Replies
13
Views
882
Calculating total Coulomb force vector ?
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top