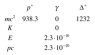joriarty
- 61
- 0
Homework Statement
Consider the following reaction that is possible when a proton (p+) collides with a photon (γ):
p+ + γ → ∆+.
Suppose that the photon is a cosmic microwave-background (CMB) photon of energy 2.3 × 10−4eV. Calculate the minimum energy that the proton must have for this reaction to take place. m∆ = 1232eV/c2.
Hints:
• The minimum energy will be for a head-on collision. Be careful with the signs of the momenta when doing the calculation.
• The answer is a very large energy, so you will be able to make the approximation that the the proton energy is much bigger than it’s rest energy.
• You might find it interesting to look up Greisen-Zatsepin-Kuzmin limit. (is this relevant?)
Homework Equations
K = E − mc2
E2 −(pc)2 =(mc2)2
The Attempt at a Solution
(See attached table)
I am thinking that because I'm after the minimum energy of the proton for a head on collision, would this mean that the delta baryon is going to have zero kinetic energy and momentum thus a total energy 1232 MeV?
I can then say that the proton has momentum pc = -2.3*10-10MeV. But that just makes the energy of the proton also equal to 938.3 MeV within the precision of my calculator. That's not right, I should get Eproton>>mprotonc2.
Where to now? Does the change in mass of 293.7 MeV have anything to do with this?
Thanks!