gregorspv
- 6
- 0
- Homework Statement
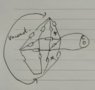
- An octahedron is made of wire, where an edge has resistance R. What is the resistance between two adjacent points?
- Relevant Equations
- Kirchhoff's rules, in parallel and in series resistance.
A sketch of the setup and the equivalent circuit are attached.
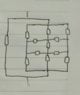
I believe the correct way to solve this is to redraw the circuit as shown in Fig. 3 and then remove the connections between evidently equipotential points, which reduces the problem to a familiar setup of in parallel and in series resistors.
However, the circuit may also be redrawn as shown in Fig. 4 where there are also two lines connecting equipotential points, yet if one removes them, an incorrect solution is obtained.
How do I then know, when such connections are removable? I have encountered a statement that such a connection must lie on the circuit's axis of symmetry and this seems to do the trick in this example, but I don't understand why it works that way.
Please excuse the formatting, I'm sadly on mobile at the moment.
I believe the correct way to solve this is to redraw the circuit as shown in Fig. 3 and then remove the connections between evidently equipotential points, which reduces the problem to a familiar setup of in parallel and in series resistors.
However, the circuit may also be redrawn as shown in Fig. 4 where there are also two lines connecting equipotential points, yet if one removes them, an incorrect solution is obtained.
How do I then know, when such connections are removable? I have encountered a statement that such a connection must lie on the circuit's axis of symmetry and this seems to do the trick in this example, but I don't understand why it works that way.
Please excuse the formatting, I'm sadly on mobile at the moment.