71GA
- 208
- 0
While dealing with a circling particle in an spherical symetric potential our professor said that we can replace an operator of ##z## component of angular momentum ##\hat{L}_z## with the expectation value - he denoted it just ##L_z## - of the angular momentum if ##L_z## is constant. Why is that?
So we first had this equation:
\begin{align}
\underbrace{\psi (r,\varphi,\vartheta)}_{\rlap{\text{w. f. in spherical coordinates}}} &= \exp\left[\hat{L}_z \frac{i}{\hbar}\, \varphi\right] \underbrace{\psi (r,0,\vartheta)}_{\rlap{\text{w. f. in spherical. coordinates at $\varphi=0$}}}
\end{align}
and we got this one (notice that there is no operator over an ##L_z##):
\begin{align}
\psi (r,\varphi,\vartheta) &= \exp\left[L_z \frac{i}{\hbar}\, \varphi\right] \psi (r,0,\vartheta)
\end{align}
Anyway here is the spherical coordinate system we ve been using all the time (the blue spherical aure is supposed to be a spherical potential...):
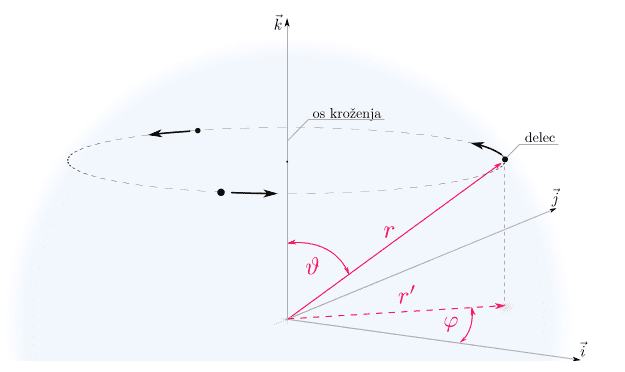
So we first had this equation:
\begin{align}
\underbrace{\psi (r,\varphi,\vartheta)}_{\rlap{\text{w. f. in spherical coordinates}}} &= \exp\left[\hat{L}_z \frac{i}{\hbar}\, \varphi\right] \underbrace{\psi (r,0,\vartheta)}_{\rlap{\text{w. f. in spherical. coordinates at $\varphi=0$}}}
\end{align}
and we got this one (notice that there is no operator over an ##L_z##):
\begin{align}
\psi (r,\varphi,\vartheta) &= \exp\left[L_z \frac{i}{\hbar}\, \varphi\right] \psi (r,0,\vartheta)
\end{align}
Anyway here is the spherical coordinate system we ve been using all the time (the blue spherical aure is supposed to be a spherical potential...):
Last edited: