Saladsamurai
- 3,009
- 7
!Resistance/Circuit Help Badly Needed!
I am doing a circuit lab with the voltage and resistors shown. I have already measured the currents across each resistor, but now I need to use some of the theory that we have learned in class. Here is an image of the original circuit.
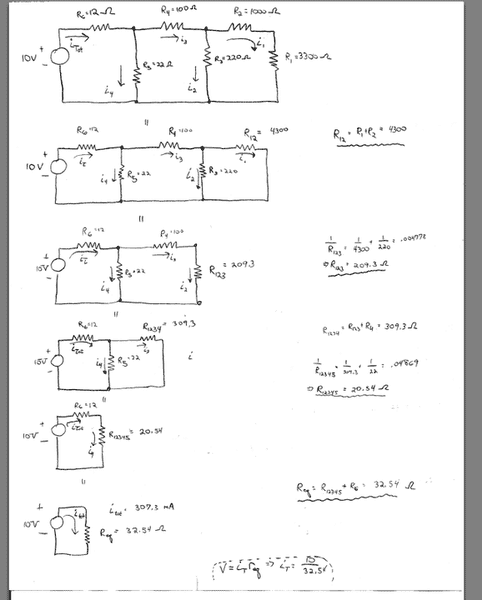
As you can see I have reduced it to a single equivalent circuit.
Now I am working backwards to try and find the currents shown. Now keep in mind that the index for the current i may not be the same index as its respective resistor... that is, i_1 does not necessarily coincide with R_1. I realize that that is annoying, but I did not type up the lab!
Now can someone help me to just find i_4 for now. I know that the current across R_{eq} is 307.3 mA.
I also know that (working backwards) that R_{eq} was made up from R_{6}+R_{12345} which were in series with each other.
So shouldn't the current across R_{12345} be the same as the i_total ? Thus making i_4=i_total=307.3 mA
Now I am pretty sure that I am not correct in saying this (because my measure currents dictate so) but I am not sure why?
Also, it says to find the currents sing the "Ladder Method"...I am assuming the above is just that.
I also have to find the currents using the "Scale Factor Method"... can someone clue me into how to do that one? I know it has to do with making an assumption and then calculating the currents based on it and this in turn leads to a scale factor.
Homework Statement
I am doing a circuit lab with the voltage and resistors shown. I have already measured the currents across each resistor, but now I need to use some of the theory that we have learned in class. Here is an image of the original circuit.
As you can see I have reduced it to a single equivalent circuit.
Now I am working backwards to try and find the currents shown. Now keep in mind that the index for the current i may not be the same index as its respective resistor... that is, i_1 does not necessarily coincide with R_1. I realize that that is annoying, but I did not type up the lab!
Now can someone help me to just find i_4 for now. I know that the current across R_{eq} is 307.3 mA.
I also know that (working backwards) that R_{eq} was made up from R_{6}+R_{12345} which were in series with each other.
So shouldn't the current across R_{12345} be the same as the i_total ? Thus making i_4=i_total=307.3 mA
Now I am pretty sure that I am not correct in saying this (because my measure currents dictate so) but I am not sure why?
Also, it says to find the currents sing the "Ladder Method"...I am assuming the above is just that.
I also have to find the currents using the "Scale Factor Method"... can someone clue me into how to do that one? I know it has to do with making an assumption and then calculating the currents based on it and this in turn leads to a scale factor.
Last edited: