Resistance of a semicircular conductor with a rectangular cross section

[Basel H]

Homework Statement

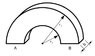
There is a conductor with the square-shaped area. the Radii are r₁ , r₂ with width b and resistivity $\rho_R$.
Find the resistance R between A and B

2. Homework Equations
$I = \iint_A\vec J \cdot d \vec A$
$\vec J = \kappa \vec E$
$\vec E = \rho \vec J$
$V = \int\vec E\cdot d\vec s$
$V = IR$

The Attempt at a Solution

$I = \iint_A\vec J \cdot d \vec A = Jb(r_2-r_1)$
$\vec J = {\frac{I}{b(r_2-r_1)}}\hat e_\theta$
$\vec E = \rho_R \vec J = (\rho_R I/b(r_2-r_1) ) \hat e_\theta$
$V = \int_0^\pi \vec E\cdot d\vec s$
$d \vec s = r d\theta \hat e_\theta$
$V = {\frac{\pi \rho_R I r}{b(r_2-r_1)}}$
The Total Voltage
$\int d V = \int {\frac{\pi \rho_R I d r}{b(r_2-r_1)}}$[/B]
After integration over $[r_1, r_2]$
$V = IR = {\frac{\pi \rho_R I}{b}}$
$R = {\frac{\pi \rho_R }{b}}$
I don't know, if the solution is right. It is a bit weird since R is not dependent of the Radii but the units are right.
I hope someone can clear my confusion and help me :)

 

[scottdave]

Do you think that the radii should play a role. It would seem so at first glance. Consider some extremes. One case I can think of: what if r2 is just a little bigger than r1, but both r1 and r2 are very large (you essentially have a very long wire). What happens if r1 and r2 are very small?

I was thinking of approaching the problem this way: what if you slice it into thin semicircles, then find the conductance of a semicircular slice (conductance is reciprocal of resistance). You can sum up (integrate) all of these parallel conductances, since conductances in parallel just add.
Once you have an expression for conductance, just take the reciprocal to find the resistance. I haven't worked all the calculations through, but the radii do play a role, in this situation.