Resistor circuit, potential drop and time

[scholio]

Homework Statement

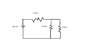
a 200 volts battery is connected to three resistors as shown, see attachment.

a) what is the potential drop across the 32 ohm resistor?

b) the 10 ohm resistor is immersed in 60 grams of water at 20 deg celsius. how long much current flow for the water to reach 40deg celsius. assume that there is not heat loss from the water through the walls of the container.

Homework Equations

parallel resistors 1/R = 1/R_1 + 1/R_2

series resistors R = R_1 + R_2

potential V = IR where I is current, R is resistance

QV/t = I^2R where Q is charge, t is time

The Attempt at a Solution

part a. first i found the parallel resistor circuit between the 10 and 40 ohm resistor, getting 8 ohms,

then i connected the new 8ohm resistor to the 32 ohm and got a single resistor of 40 ohms.

i tried using V =IR to solve for potential, but it didn't work

QV/t = I^2R , couldn't use that and solve for V because i didn't have time

does the problem involve a temperature coefficient of resistivity of water to solve for part b?

any help, for either part, appreciated

 

[Andrew Mason]

part a. first i found the parallel resistor circuit between the 10 and 40 ohm resistor, getting 8 ohms,

Correct.

then i connected the new 8ohm resistor to the 32 ohm and got a single resistor of 40 ohms.

i tried using V =IR to solve for potential, but it didn't work

You first have to determine the current. What is the current flowing through the 32 ohm resisitor (hint: it is a function of the total voltage and total resistance)? Then use V=IR to determine the voltage across the 32 ohm resistor.

QV/t = I^2R , couldn't use that and solve for V because i didn't have time

does the problem involve a temperature coefficient of resistivity of water to solve for part b?

any help, for either part, appreciated

Why use QV/t for power? Q/t = current = I so:

$$P = VI = I^2R$$

AM