Resonance Experiment:-Air Tube Column

[andyrk]

We know that we get first resonance when the length of the air column is λ/4. We get second resonance when the length of the air column is 3λ/4. This is because we get a node at the surface of the water after λ/4 distance in the first case and 3λ/4 in the second case. My question is that what happens if we take the length of the air column not be λ/4 or 3λ/4 but somewhere in between say λ/2. How would the wave diagram look like? I am posting all the three cases' diagrams. Please verify if the last diagram (λ/2 case) would be like the one I have posted or not? I think not because we can never get an anti-node at an open end. So how would the wave diagram look like? Thank you, reply soon!

 

[STEMucator]

We know that we get first resonance when the length of the air column is λ/4. We get second resonance when the length of the air column is 3λ/4. This is because we get a node at the surface of the water after λ/4 distance in the first case and 3λ/4 in the second case. My question is that what happens if we take the length of the air column not be λ/4 or 3λ/4 but somewhere in between say λ/2. How would the wave diagram look like? I am posting all the three cases' diagrams. Please verify if the last diagram (λ/2 case) would be like the one I have posted or not? I think not because we can never get an anti-node at an open end. So how would the wave diagram look like? Thank you, reply soon!

I'm presuming you're working in a column that has one end closed and one end open.

Your $\lambda/2$ drawing is wrong. The $\lambda/2$ diagram you have is actually the $3\lambda/4$ diagram which means that your $3\lambda/4$ drawing is also wrong ( Completely wrong in general actually. Think about it ).

You can't really consider $\lambda/2$ in the case of a column with one end closed and the other open. Although I will mention that $\lambda/2$ is the first resonant length if BOTH ends of the column are open.

 

[andyrk]

Why can't we consider λ/2 in case of one end open and the other closed? What's stopping us to do so?

 

[STEMucator]

Why can't we consider λ/2 in case of one end open and the other closed? What's stopping us to do so?

The shortest column with one end closed and one end open that can produce resonance has a length of $\lambda/4$.

That being said, there are only certain wavelengths which will produce resonance in the closed column. These resonant wavelengths for a closed column can be found using the relation :

$L_1 = \frac{\lambda}{4}$
$L_n = L_{n-1} + \frac{\lambda}{2}$

Using this you can find the $n^{th}$ resonant length when one end is closed and one end is open.

 

[PeterO]

We know that we get first resonance when the length of the air column is λ/4. We get second resonance when the length of the air column is 3λ/4. This is because we get a node at the surface of the water after λ/4 distance in the first case and 3λ/4 in the second case. My question is that what happens if we take the length of the air column not be λ/4 or 3λ/4 but somewhere in between say λ/2. How would the wave diagram look like? I am posting all the three cases' diagrams. Please verify if the last diagram (λ/2 case) would be like the one I have posted or not? I think not because we can never get an anti-node at an open end. So how would the wave diagram look like? Thank you, reply soon!

For the closed tube you are using, the wave pattern you draw HAS to have node at the surface, and an antinode at the open end of the tube.. Your λ/2 diagram has an antinode at the open end and also at the surface. Your 3λ/n looks more like the 5λ/2 pattern.

 

[Basic_Physics]

The patterns you are drawing is for standing waves. They show how the amplitude of vibration of the molecules vary throughout the depth of the tube. We get large amplitude vibrations at the antinodes and no vibration of the molecules at the point where nodes are found in the tube. Sound are longitudinal waves. That is the vibration of the molecules are up and down in the diagram of the tubes and not sideways. The standing waves patterns that can form in the tube will then have a node at the water surface and an antinode at the open end of the tube. Only part of the whole wave fits into the tube. These standing wave patterns are formed by the interference between the wave traveling down the tube and wave reflected back up the tube. Constructive interference only occurs for wavelengths that are such that length of tube is equal to 1/4 λ, 3/4 λ, 5/4 λ ... For these standing wave patterns have nodes at the water surface and antinodes at the top. Resonance will only occur for these wavelengths. At these wavelengths the standing wave patterns are formed. These patterns do not move like waves, they are stationary, although the molecules are still vibrating like i explained. Incidentally the antinodes are located a short distance outside of the tube. The amount that it extends outside depends on the diameter of the tube. This is called the end correction. So the relationship is actually

L + c = n/4 λ n = 1,3,5...

where L is the length of the tube and c the end correction.

 

[barryj]

The discussion above assumes that we are talking about resonance. Nodes and anti-nodes will apear and be stationary if the tube is resonate at the given frequency. If we excite the tube at a different, non-resonant frequency, certainly there will be some sort of response but you will not see a stationary series of nodes and anti-nodes. If the exciting frequency is slightly different from resonance, I think, I repeat think you will see a slowly changing pattern.

 

[Basic_Physics]

Sure, sound of any wavelength can propagate in the tube, but, only for these wavelengths will the tube respond or resonate.

 

[tayliangcai]

Question

The discussion above assumes that we are talking about resonance. Nodes and anti-nodes will apear and be stationary if the tube is resonate at the given frequency. If we excite the tube at a different, non-resonant frequency, certainly there will be some sort of response but you will not see a stationary series of nodes and anti-nodes. If the exciting frequency is slightly different from resonance, I think, I repeat think you will see a slowly changing pattern.

Hi, I am new here. I actually don't understand the pattern of the standing waves if there are situation like "If we excite the tube at a different, non-resonant frequency", will there are always node at the water surface and antinode at the open end?

Secondly, if it is, then, at a certain length (in the tube), which producing a non-resonant frequency, will the wavelength change? Because since the wave pattern have to be in " node at water surface, antinode in open end" pattern, I can't think a second way by either changing wavelength or adding more "complete wave count" (I don't know the actual term :P).
If is does by adding more "complete wave count", where wavelength is fixed, I am sure that the wave pattern will not fulfill the pattern aforementioned (node at the water surface and antinode at the open end) at all the length in the tube.


So I do make a hypothesis here where the wave might change it's wavelength, but then I met a new problem, how do the wave itself know that, the tube already have a suitable length for it to have a second lambda, instead of just keep on increasing it's wavelength ?

Sorry for the poor English command XD. By the way I do attach a picture here if my words doesn't deliver my message. (Note that L2 > L1)

Thank you.

 

[PeterO]

Hi, I am new here. I actually don't understand the pattern of the standing waves if there are situation like "If we excite the tube at a different, non-resonant frequency", will there are always node at the water surface and antinode at the open end?

Secondly, if it is, then, at a certain length (in the tube), which producing a non-resonant frequency, will the wavelength change? Because since the wave pattern have to be in " node at water surface, antinode in open end" pattern, I can't think a second way by either changing wavelength or adding more "complete wave count" (I don't know the actual term :P).
If is does by adding more "complete wave count", where wavelength is fixed, I am sure that the wave pattern will not fulfill the pattern aforementioned (node at the water surface and antinode at the open end) at all the length in the tube.


So I do make a hypothesis here where the wave might change it's wavelength, but then I met a new problem, how do the wave itself know that, the tube already have a suitable length for it to have a second lambda, instead of just keep on increasing it's wavelength ?

Sorry for the poor English command XD. By the way I do attach a picture here if my words doesn't deliver my message. (Note that L2 > L1)

Thank you.

The key to your problem I have highlighted in red. The operator cannot choose to "excite" the tube at a "non-resonant" frequency. You can create a not resonant frequency sound at/near the tube but no resonance (excitation?) will occur.
Thus your second and third parts don't apply.

Peter

 

[PeterO]

Hi, I am new here. I actually don't understand the pattern of the standing waves if there are situation like "If we excite the tube at a different, non-resonant frequency", will there are always node at the water surface and antinode at the open end?

Secondly, if it is, then, at a certain length (in the tube), which producing a non-resonant frequency, will the wavelength change? Because since the wave pattern have to be in " node at water surface, antinode in open end" pattern, I can't think a second way by either changing wavelength or adding more "complete wave count" (I don't know the actual term :P).
If is does by adding more "complete wave count", where wavelength is fixed, I am sure that the wave pattern will not fulfill the pattern aforementioned (node at the water surface and antinode at the open end) at all the length in the tube.


So I do make a hypothesis here where the wave might change it's wavelength, but then I met a new problem, how do the wave itself know that, the tube already have a suitable length for it to have a second lambda, instead of just keep on increasing it's wavelength ?

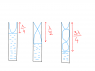
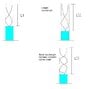
Sorry for the poor English command XD. By the way I do attach a picture here if my words doesn't deliver my message. (Note that L2 > L1)

Thank you.

Perhaps my first answer mis-read your idea - but the "when producing a non-resonant frequency" is an issue.

I think you are confusing standing waves (in general) and resonance (a very special case of standing waves).

Standing waves are produced when ever two waves, of equal wavelength and 9at least similar) amplitude, traveling in opposite directions, pass through each other.

One way to achieve this is to have two loud speakers connected to a single signal generator/amplifier set-up facing each other.

The sound produced by each speaker loses intensity as the sound travels from the speakers, so near either of the speakers you will mainly hear the near speaker, with the sound slightly increased/decreased by the effect of the other, distant speaker. But, at a position near the middle, the two intensities will have each decayed about the same so as you move along the line joining the speakers you will hear successive loud (anti-node) and soft (node) points.

Another way to notice the same effect is to have a single speaker directed at a reflecting wall (side of a building). This time the sound approaching the wall forms a standing wave with the sound reflecting from the wall. Again, if you move too far from the wall, the large intensity sound passing from the speaker, will "overwhelm" the smaller intensity sound reflected from the wall so you might not notice the nodes and antinodes if too far from the wall. (eg. if the speaker is 20m from the wall, and you are listening from a point 10m from the wall, the direct sound has traveled only 10m to get to you (losing a certain amount of intensity on the way) while the reflected sound has traveled 30m (speaker - wall - you) losing much more intensity.

The resonance in the tube is closely related to the sound reflecting off the wall. The sound wave travels down the tube, reflecting off the end (water surface) and coming back. Once that sound reaches the open end again, a certain amount transmits out of the tube (that's why we hear it) while the rest reflects back down the tube - only to bounce back and away we go.

[Some people get hung up on how reflection from the open end actually happens - but it is sufficient here to acknowledge it does.
** proof: Get a 1m long post tube (the sort they use to mail pictures/calendars/charts through the post: snail-mail) Remove both plastic ends and slap one end with the palm of you hand. You will hear a dull, decaying resonance which lasts perhaps only 0.1 seconds. However, in 0.1 seconds, sound travels 33m! So before the sound has "dispersed" from the tube, it has traveled 33 times along the tube - which can only occur if a fair amount of the sound wave is reflecting back into the tube (though not all of it - or the sound would go on for ever)]

Back to the problem at hand; let us suppose that 100% of the sound energy reflects from the water surface, 80% reflects from the open end, and none is lost as the wave travels along the tube.

We start by producing a small sound at the open end of the pipe. (we begin with 100%)
That 100% reflects off the water
Back an the open end 80% reflects 20% disperses.
BUT, we are still producing our stimulus, so another 100% is added to the 80% --> 180%
That 180% reflects off the water, then 36% disperses and 144%+100% goes back down the tube (244%)
Next time 20% of 244% disperses, and 80% of 244% (plus another 100%) heads back along the tube.
Eventually the sound in the tube will be of sufficient intensity that the amount dispersing equals the amount of the stimulus so stability is reached.
Thus a quiet humm into the pipe results in a reasonably load sound.

OF course, adding a little extra to the reflecting waves has to be done at just the right time. It is no good adding a small compression to an existing rarefaction - that will just get rid of the wave even quicker. A small compression has to be added to an existing compression. That is why there is only certain frequencies of stimulus that work for each given tube: - the resonant frequencies.
For other frequencies it simply does not work - so we don't have to consider them.

Peter

 

[tayliangcai]

Sorry for the late reply, Peter. Thanks for the explanation. Your explanation bring me to a higher level of understanding the resonance.

For other frequencies it simply does not work - so we don't have to consider them.

But I am curious for that -- how does them looks like in a tube? By the way thanks again.

 

[ehild]

Depending on the exciting frequency, the motion can look quite irregular. Near a resonant frequency, you can see a slowly moving pattern. See