Resultant force and its point of action

[MCTachyon]

Homework Statement

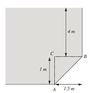
A storage tank has the cross-sectional shape shown attached and is of 1m breadth. Calculate the resultant force acting on the inclined surface AB and its point of action.

The density of the liquid is 900kgm^–3 and take g = 9.81ms^–2.

Homework Equations

P = ρgh
F = ρA
Point of action = h_c + (I_g Sin(θ)² / A h_c)

The Attempt at a Solution

Length of AB:

Tanθ = (O/A)
θ = Tan^-1 (1.5/1)
θ = 56.31°

Cos(56.31) = 1/AB
AB = 1/Cos(56.31)
AB = 1/0.5547
AB = 1.8m

Pressure at centroid of AB:

P = ρgh
P = 900 x 9.81 x (4 + (1.8/2))
P = 900 x 9.81 x 4.9
P = 432621Pa

Resultant force at AB:

F = ρA
F = 432621 x (1.8 x 1)
F = 77818N
F = 77.82kN

This is bit when I get a bit lost.

Point of Action:

= h_c + (I_g Sin(θ)² / A h_c)

Where I_g = db/12 = 1.8/12 = 0.15

= 4.9 + (0.15 x Sin(90-56.31)² / 1.8 x 1 x 4.9)

= 4.9 + 0.00523

= 4.90523m

Therefore force of 77.82kN is acting 4.90523m from top of storage tank.
------------------------------------------------------------------------------------------------------

Am I on the right track with my method? Pretty confident till working out the Point of Action.

 

[haruspex]

θ = 56.31°

It is rarely necessary to find the angle. You can go straight from one trig ratio to another. E.g. use Pythagoras.

P = 900 x 9.81 x (4 + (1.8/2))

Pressure varies as depth. The 1.8m is not vertical.

Where Ig = db/12 = 1.8/12 = 0.15

This doesn't seem right. Shouldn't there be a quadratic term? Certainly it seems like the resulting equation for point of action is dimensionally inconsistent...

... Or maybe I am misreading it. Please make it clearer by use of parentheses and define all the variables.

 

[MCTachyon]

Thank you.

Lots of food for thought there. I will go back and retry.

Thanks again.

 

[MCTachyon]

Second attempt:

Length of AB:

Pythagorean Theorem:

A² + B² = C²

C = √ (1² + 1.5²)
C = √3.25
C = 1.8m

Pressure at centroid of AB:

P = ρgh

P = 900 x 9.81 x (4 + (1/2))
P = 39731 Pa
P = 39.73 kPa

Resultant force at AB:

F = ρA
A = (h x b) / 2
F = 39731 x ((1 x1.5) / 2)
F = 39731 x 0.75
F = 29798 N
F = 29.80 kN

Point of Action:

Area Moment of Inertia:

I_y = I_R + Ar²

Where:

I_R = (d x b³) / 36

I_R = (1 x 1.5³) / 36
I_R = 3/32 = 0.09375m⁴

Therefore:

I_y = 3/32 + ((1 x 1.5) / 2) x 4.5²
I_y = 15.28m⁴

Radius of Gyration:

R_y = √(I / A)
R_y = √ (15.28 / 0.75)
R_y = √ 20.37
R_y = 4.513m

Therefore force of 29.80 kN is acting 4.513m from top of storage tank.

-----------------------------------------------------------------------------------------------------------

Any closer to sussing out the method?

Thanks for your help with this.

 

[haruspex]

F = ρA

PA not ρA.

A = (h x b) / 2

(d x b3) / 36

What shape do you think the area is?

 

[MCTachyon]

What shape do you think the area is?

ABC, so a right angled triangle.

 

[haruspex]

ABC, so a right angled triangle.

That's not how I interpret the diagram.
C seems to be just a reference point for showing the width and height of the sloped section. The text says it is a cross-section, implying the "breadth 1m" is into the page. The area of interest is therefore a rectangle, seen side-on as AB.

 

[MCTachyon]

Right then, this is starting to make some sense now.

It is late where I am, I will come back tomorrow with some new numbers and see if this info has put me on the right track.

Thanks again for your help.

 

[David Lewis]

With vectors you have a point of application, and a line of action.

 

[MCTachyon]

Third attempt:

Pressure at centroid of AB:

P = ρgh

P = 900 x 9.81 x (4 + (1/2))
P = 39731 Pa
P = 39.73 kPa

Resultant force at AB:

F = PA
A = (h x b)
F = 39731 x (1 x1.5)
F = 39731 x 1.5
F = 59597 N
F = 59.60 kN

Point of Action:

Area Moment of Inertia:

I_y = I_R + Ar²

Where:

I_R = (d x b³) / 12

I_R = (1 x 1.5³) / 12
I_R = 9/32 = 0.28125m⁴

Therefore:

I_y = 9/32 + (1 x 1.5) x 4.5²
I_y = 30.66m⁴

Radius of Gyration:

R_y = √(I / A)
R_y = √ (30.66 / 1.5)
R_y = √ 20.44
R_y = 4.52m

Therefore force of 59.60 kN is acting 4.52m from top of storage tank.

------------------------------------------------------------------------------------------------------------------

Getting closer?

Thanks again for all your help.