mldavis086
- 10
- 0
Homework Statement
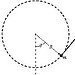
A 0.30-kg mass attached to the end of a string swings in a vertical circle
(R = 1.6 m), as shown. At an instant when θ = 50°, the tension in the string is
8.0 N. What is the magnitude of the resultant force on the mass at this instant?
http://www.flickr.com/photos/89533422@N08/8142258633/in/photostream/lightbox/
Homework Equations
m*centripetal acceleration=m*v^2/r
mg
basic trig
The Attempt at a Solution
I've figured out
mg = 2.94 N
mg sin 50 = 2.25 N (which acts opposite of the direction of the mass)
mg cos 50 =1.89 N (the tension due to gravity)
8-1.89 = 6.11 N (the tension due to motion of the mass)
8=0.3*v^2/1.6 (v=5.71 m/s)
-2.25=0.3*a (a=-7.5 m/s^2)
I'm not 100% on the last 2
But I still don't know what the resultant force is? Or even what force they are referring to. If anyone can help it would be greatly appreciated!